
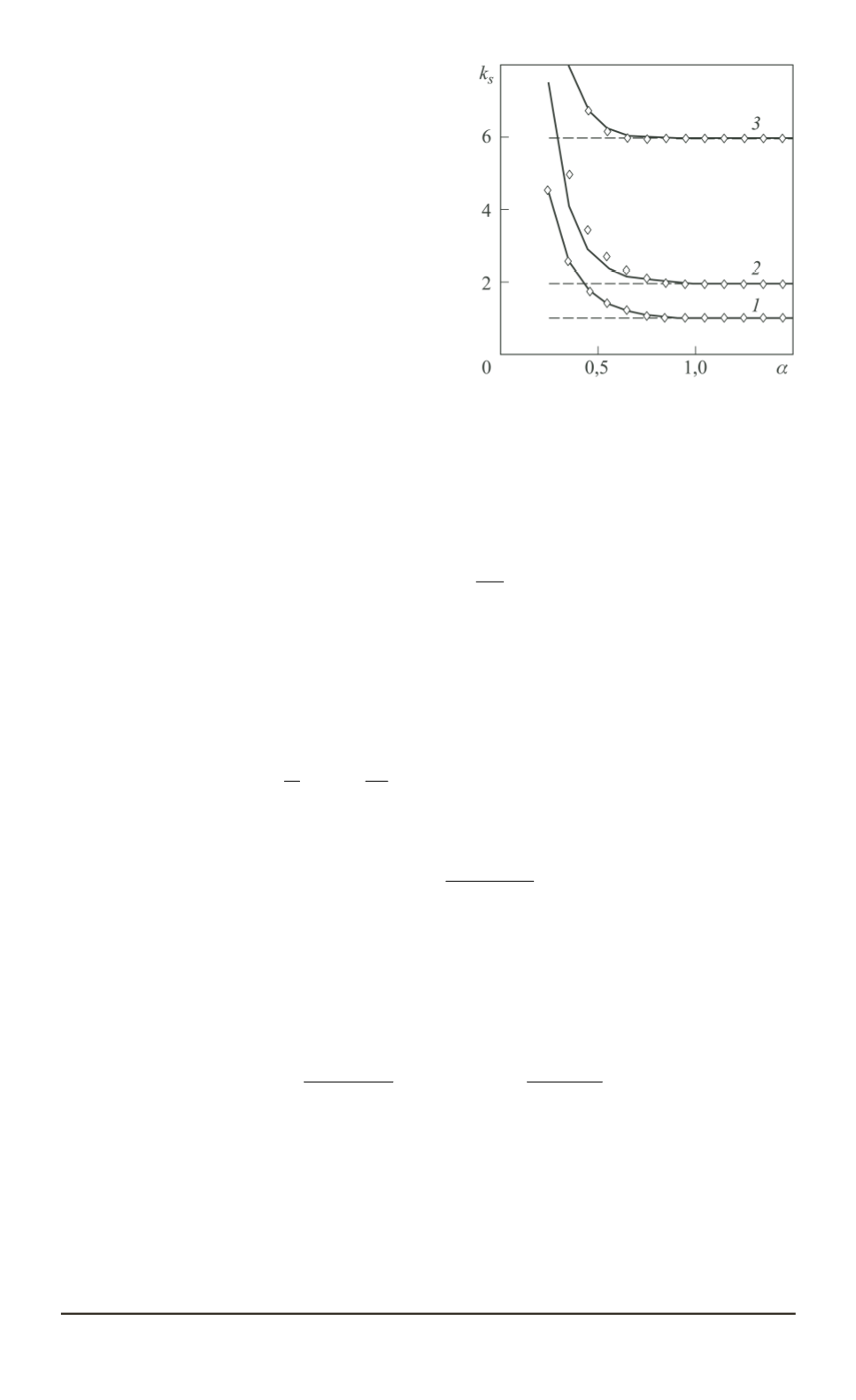
Рис. 2. Графики зависимости ко-
эффициента
k
s
от параметра
α
:
1, 2, 3
— соответственно при
γ
= 0
,
1
и
2
; —— — по выражению (4);
♦
—
по [8]; – – – — по [6]
условия устойчивости каждой пане-
ли, на которые делит пластину ребро
(см. рис. 1, панели
1
и
2
)
σ
max
i
≤
[
σ
c
pi
]
.
(7)
Здесь
σ
c
pr
и
σ
c
pi
— критическое
напряжение для системы “пласти-
на + ребро” и для
i
-й панели;
σ
max
i
—
максимальное по абсолютной величи-
не сжимающее напряжение в
i
-й пане-
ли пластины.
Критическое напряжение
σ
cpi
вы-
числяем по формуле (3), используя
геометрические параметры и условия
нагружения
i
-й панели. Так, критиче-
ское напряжение для панели
1
(см.
рис. 1) находим по выражениям:
σ
c
p
1
=
k
s1
K
s
0
t
βd
2
;
(8)
k
s1
=
n
1 + (0
,
6 +
α
1
)
−
8
(1 + 0
,
42
γ
1
) +
+ 1
−
2 (1 +
α
1
)
−
7
0
,
52
γ
3
1
o
ζ
s
;
(9)
здесь
γ
1
=
βγ
;
α
1
=
α
β
;
β
=
d
1
d
.
Критическое напряжение для панели
2
(см. рис. 1) вычисляется как
σ
c
p
2
=
k
s2
K
s
0
t
(1
−
β
)
d
2
;
(10)
k
s2
=
n
1 + (0
,
6 +
α
2
)
−
8
(1 + 0
,
42
γ
2
) +
+ 1
−
2 (1 +
α
2
)
−
7
0
,
52
γ
3
2
o
ζ
s
;
(11)
γ
2
=
γ
(1
−
β
)
(1
−
γβ
)
≤
2;
α
2
=
α
(1
−
β
)
.
Если получается
γ >
2
, то следует вести расчет с учетом коррек-
тировок, приведенных после формулы (5).
Как уже отмечалось, для вычисления критических напряжений си-
стемы “пластина + ребро”
σ
c
pr
достаточно общих рекомендаций нет.
Метод конечных элементов (МКЭ) позволяет рассчитать конструкцию
сколь угодно сложной конфигурации при любых условиях нагружения,
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение” 2015. № 4 123

















