
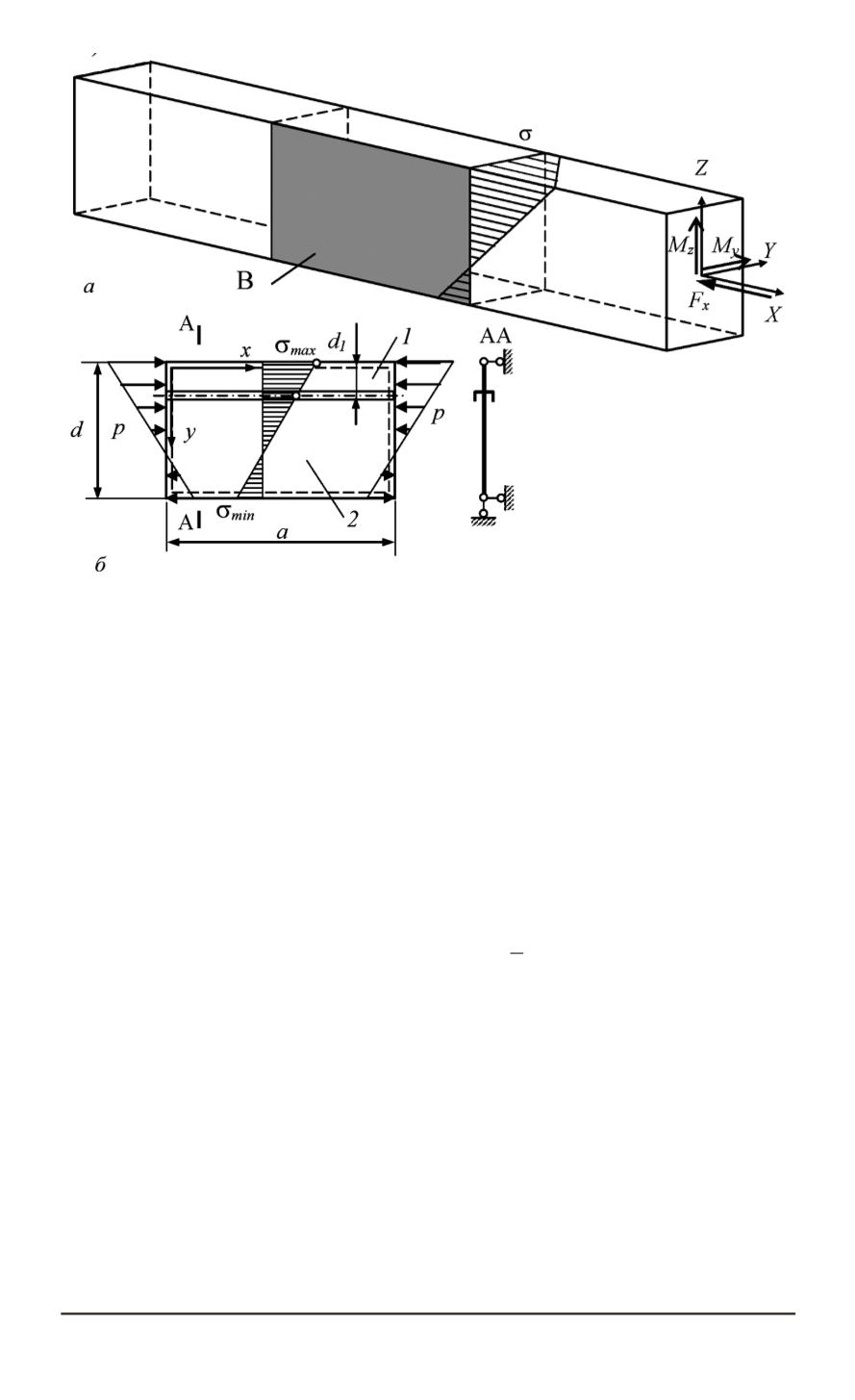
Рис. 1. Схема коробчатой балки (
a
) и модель пластины с ребром (
б
)
рис. 1,
б
), что отражает ее связь со смежными элементами. Нормаль-
ные напряжения, действующие в поперечных сечениях балки, моде-
лируются распределенной нагрузкой
p
=
tσ
, лежащей в срединной
плоскости пластины и приложенной к поперечным кромкам расчетной
пластины. Таким образом, пластина находится в условиях одноосного
напряженного состояния.
Начало локальной системы координат
x, y
зададим на кромке, ис-
пытывающей наибольшее сжатие (см. рис. 1,
б
). Для анализа устойчи-
вости линейное распределение нормальных напряжений по ширине
пластины опишем зависимостью
σ
(
y
) =
σ
max
1
−
γ
y
d
.
(1)
Здесь
σ
max
— наибольшее сжимающее напряжение на кромке
y
= 0
;
γ
= 1
−
σ
min
/
σ
max
— параметр нагружения пластины;
σ
min
— напря-
жение на кромке
y
=
d
. В расчетах на устойчивость сжимающие
напряжения считают положительными.
Условие устойчивости такой пластины без ребра при расчете по
допускаемым напряжениям имеет вид
σ
max
≤
[
σ
c
]
,
(2)
где
[
σ
c
] =
σ
c
/
n
— допускаемое напряжение сжатия по условию устой-
чивости;
σ
c
— критическое напряжение сжатия по условию упругой
устойчивости пластины;
n
— коэффициент запаса устойчивости.
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение” 2015. № 4 121

















