
где
D
— изображение по Лапласу для дифференциальной составляю-
щей;
Y
— изображение по Лапласу для управляемого параметра;
T
F
=
T
D
N
(11)
— постоянная времени фильтра, параметр фильтра
N
= 8
. . .
10
.
Данные модификации позволяют обеспечить низкую восприимчи-
вость дифференциальной составляющей к высокочастотным измери-
тельным шумам.
Для вычисления дифференциальной составляющей используется
следующее выражение [3]:
D
(
k
) =
αD
(
k
−
1)
−
b
d
(
y
(
k
)
−
y
(
k
−
1))
.
(12)
Значения коэффициентов
α
и
b
d
зависят от способа дифференци-
рования и приведены в табл. 2.
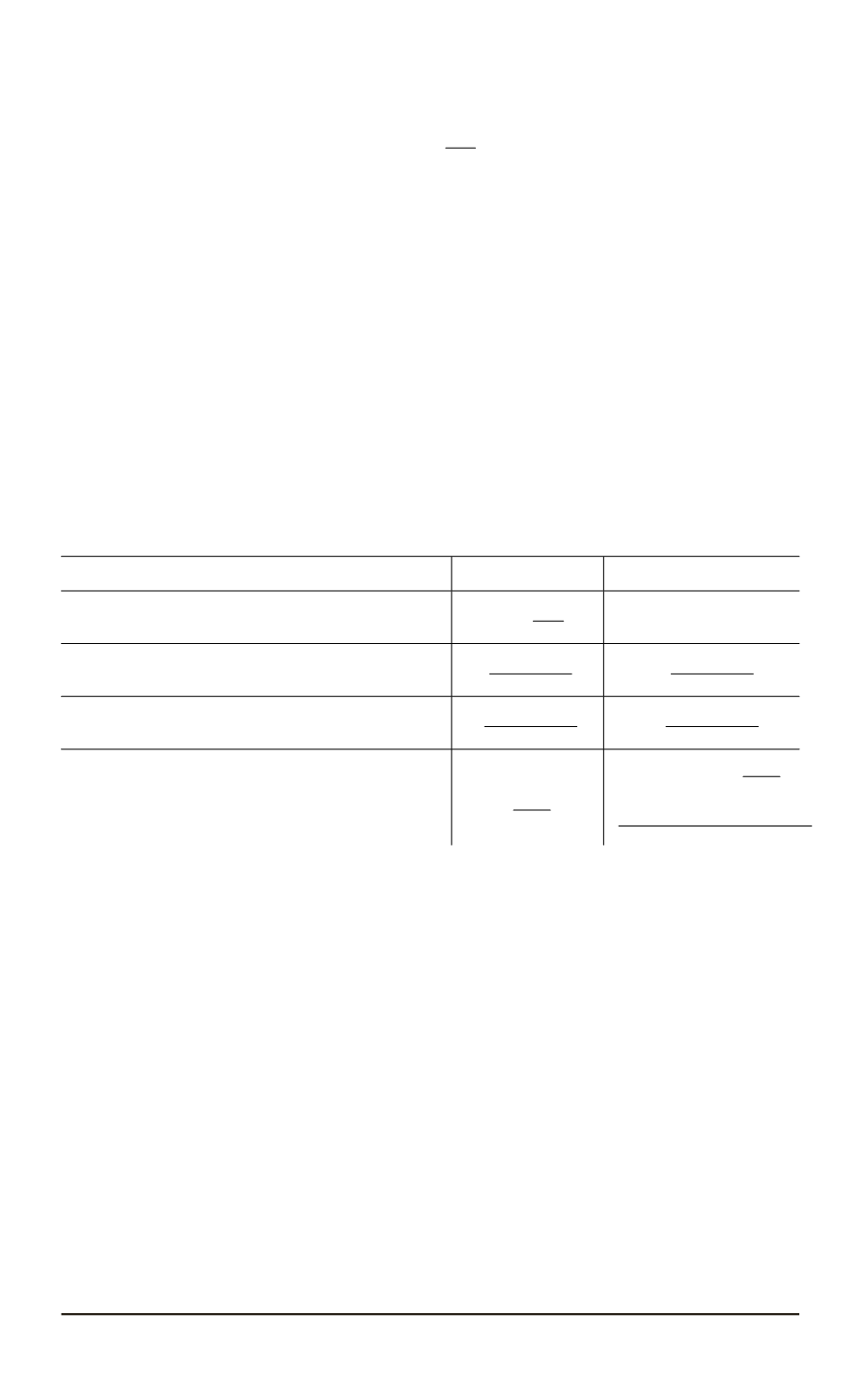
Таблица 2
Значения коэффициентов для вычисления дифференциальной составляющей
Способ дифференцирования
Коэффициент
α
Коэффициент
b
d
Метод левых прямоугольников
1
−
Nh
T
d
KN
Метод правых прямоугольников
T
D
T
D
+
Nh
KT
D
N
T
D
+
Nh
Метод средних прямоугольников
2
T
D
−
Nh
2
T
D
+
Nh
2
KT
D
N
2
T
D
+
Nh
Метод трапеций
e
−
Nh
T
D
KT
D
1
−
e
−
Nh
T
D
!
h
При малых значениях постоянной времени дифференцирования
лучшую производительность показывает метод левых прямоугольни-
ков [3]. На рис. 1 приведена структурная схема вычисления управля-
ющего воздействия с использованием данного метода.
При выполнении синтеза алгоритма регулирования на базе ПИД-
регулятора требуется определить коэффициенты, что можно выпол-
нить либо на основе опыта эксперта, либо применяя различные рас-
четные методики.
Для применения расчетных методик требуется информация о мате-
матической модели объекта. Для примера в качестве модели объекта
управления рассматривается модель дизельного двигателя ЯМЗ-238
применительно к режимам холостого хода. Параметры модели были
определены и использованы в работах [5, 6], структурная схема моде-
ли приведена на рис. 1.
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение” 2015. № 3 137

















