
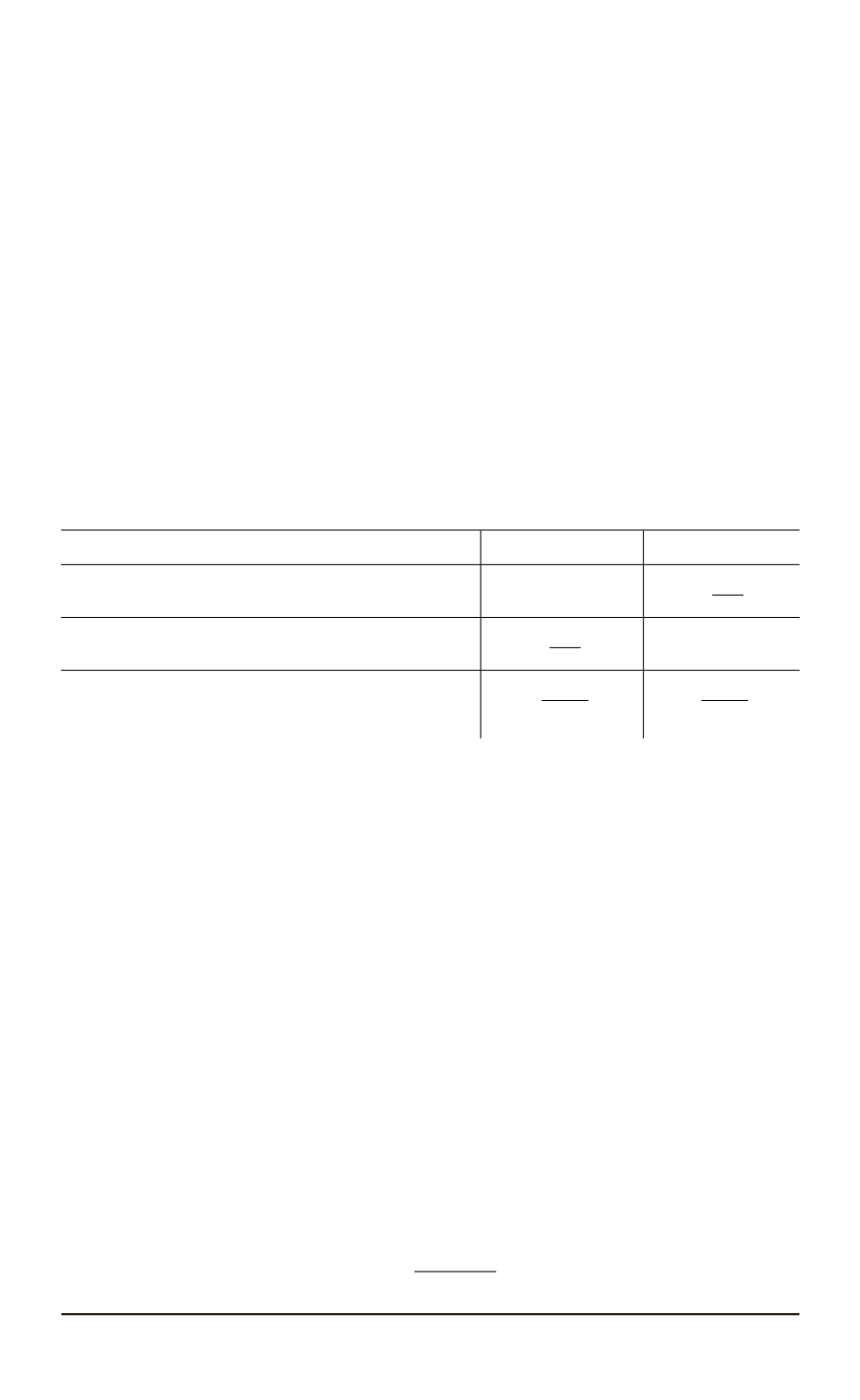
где
k
— номер дискретного значения;
P
— пропорциональная состав-
ляющая;
I
— интегральная составляющая;
D
— дифференциальная
составляющая.
Пропорциональная составляющая
P
может быть вычислена
как [3]
P
(
k
) =
K
(
br
(
k
)
−
y
(
k
))
,
(8)
где
b
— весовой фактор для учета влияния заданного значения на
пропорциональную составляющую.
Интегральная составляющая
вычисляется по выражению [3]
I
(
k
+ 1) =
I
(
k
) +
b
i
1
e
(
k
+ 1) +
b
i
2
e
(
k
)
.
(9)
Значения коэффициентов
b
i
1
и
b
i
2
зависят от способа интегрирова-
ния и приведены в табл. 1.
Таблица 1
Значения коэффициентов для вычисления интегральной составляющей
Способ интегрирования
Коэффициент
b
i
1
Коэффициент
b
i
2
Метод левых прямоугольников
0
Kh
T
I
Метод правых прямоугольников
Kh
T
I
0
Метод средних прямоугольников / Метод тра-
пеций
Kh
T
I
∙
2
Kh
T
I
∙
2
Когда ДВС работает на различных нагрузочно-скоростных режи-
мах, существует вероятность того, что управляющее воздействие ЭСУ
достигнет пределов рабочего диапазона исполнительного механизма.
В этом случае исполнительный механизм остается в неизменном поло-
жении, несмотря на изменение управляющего воздействия. Обратная
связь на данном режиме работы автоматически разрывается. Ошиб-
ка регулирования при этом продолжает накапливаться и интегральная
составляющая существенно возрастает, что негативно сказывается на
работе системы управления после вывода исполнительного механизма
из “ограничения”. В целях предотвращения подобного явления алго-
ритмом управления должно предусматриваться ограничение макси-
мального и минимального значений интегральной составляющей, а
также сброс интегральной суммы в зависимости от условий работы.
Дифференциальная составляющая
используется совместно с
фильтром низких частот согласно следующему выражению в изобра-
жениях по Лапласу:
D
=
−
sKT
D
1 +
sT
F
Y,
(10)
136 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2015. № 3

















