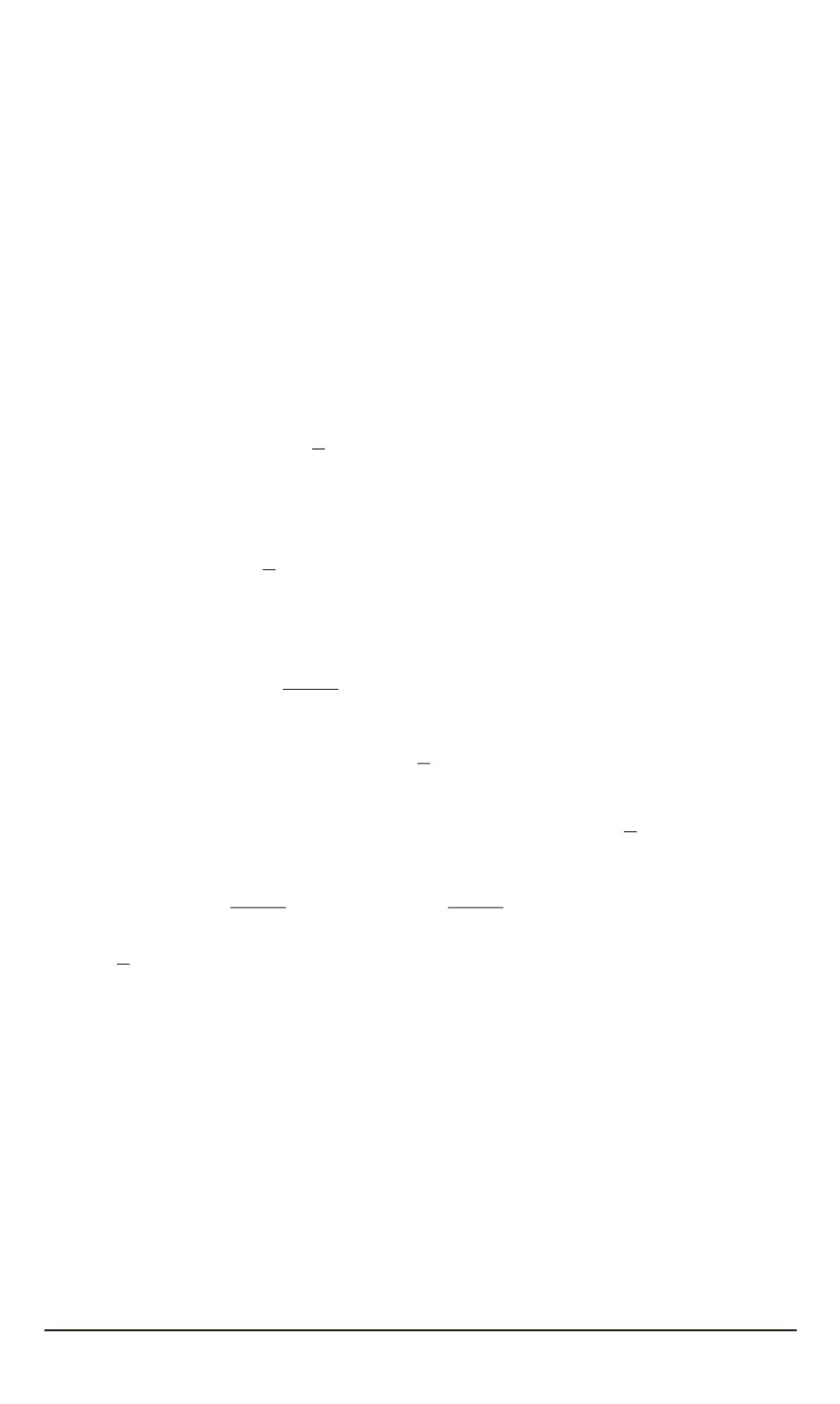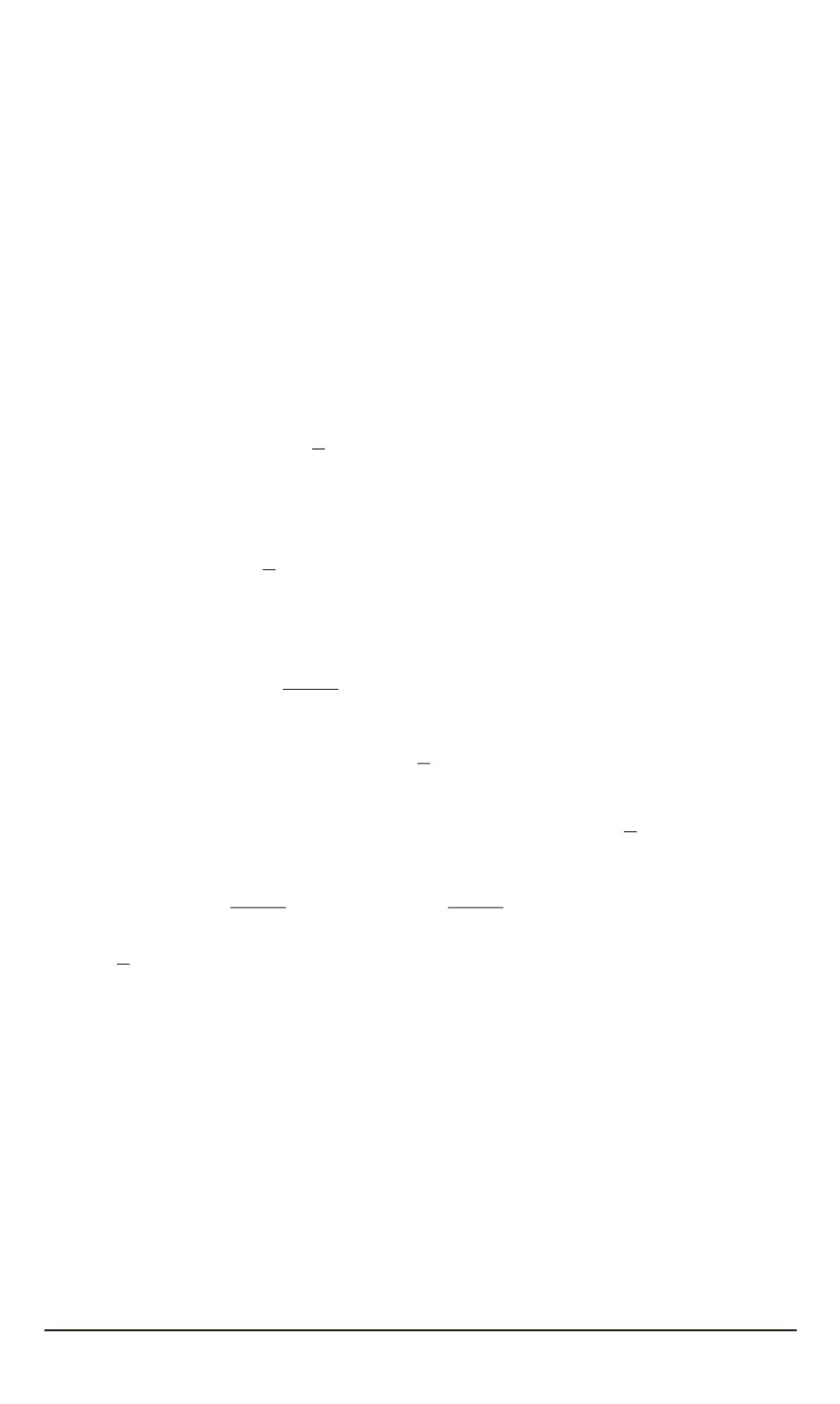
При параллельном соединении структур (звеньев) их деформации
одинаковы
F
A
= F
B
= F
,
(1)
здесь
F
— градиент вектора места (градиент деформации).
Напряжения в материале складываются из откликов структур (зве-
ньев)
σ
=
σ
A
+
σ
B
.
(2)
Статическая составляющая напряжения
σ
A
определяется соотноше-
ниями гиперупругости на основе выражения для удельной энергии
деформации материала:
W
A
=
1
2
k
(
J
−
1)
2
+ ˉ
W
A
( ˉ
I
1
C
,
ˉ
I
2
C
)
,
(3)
где
k
— модуль объемного сжатия;
J
= det F
— мера объемной
деформации;
ˉ
W
A
( ˉ
I
1
C
,
ˉ
I
2
C
)
— энергия изохорической деформации;
ˉ
I
1
C
= tr ˉC
,
ˉ
I
2
C
=
1
2
ˉ
I
2
1
C
−
ˉC : ˉC
— первый и второй инварианты
тензора меры изохорической деформации
ˉC =
J
−
2
/
3
F
T
F
.
В соответствии с выражением (3) второй тензор напряжений Пио-
лы – Кирхгофа
S
A
= 2
∂W
A
∂
C
имеет вид [6]
S
A
=
kJ
(
J
−
1)C
−
1
+ 2
ϕ
A
1
I
−
1
3
I
1
C
C
−
1
+
+ 2
ϕ
A
2
I
1
C
I
−
C
−
2
3
I
2
C
C
−
1
,
(4)
где
ϕ
A
1
=
J
−
2
/
3
∂
ˉ
W
A
∂
ˉ
I
1
c
,
ϕ
A
2
=
J
−
4
/
3
∂
ˉ
W
A
∂
ˉ
I
2
c
,
C = F
T
F
,
I
1
C
= tr C
,
I
2
C
=
1
2
(
I
2
1
C
−
C : C)
.
Переходя к истинным напряжениям Коши по формуле
σ
A
=
=
J
−
1
FS
A
F
T
, можно получить
σ
A
=
k
(
J
−
1)I + 2
J
−
1
(
ϕ
A
1
+
I
1
C
ϕ
A
2
)devB
−
2
J
−
1
ϕ
A
2
dev(BB)
,
(5)
где
B = FF
T
— тензор меры деформации Фингера [6], символ dev
обозначает девиатор тензора.
В настоящей работе для полиуретана использовались два варианта
функции энергии изохорической деформации:
•
традиционный для резины потенциал Муни – Ривлина
ˉ
W
A
=
C
A
10
ˉ
I
1
C
−
3 +
C
A
01
ˉ
I
2
C
−
3 ;
(6)
50 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2014. № 6