времени. Таким образом, для заданного закона нагружения
σ
1
(
t
)
опре-
деляются кратности удлинений
λ
1
,
λ
B
1
e
как функции времени.
Результаты моделирования.
Значения параметров
C
A
10
,
C
A
01
моде-
ли Муни – Ривлина (21) и параметров
G
A
,
λ
A
lock
модели Арруда – Бойс
(22) подбирались так, чтобы по возможности точнее описать кривую
статического нагружения полиуретана, показанную на рис. 1. Относи-
тельные укорочения ограничивались значением 35%. Для поиска ука-
занных параметров использовался алгоритм минимизации функции
отклонений расчетных величин
σ
1
(
λ
1
)
от результатов эксперимента
методом Нелдера –Мида, подробно изложенный в работе [12]. Неза-
висимо от этого для повышения достоверности осуществлялся поиск
значений с помощью встроенных средств программы Ansys. В резуль-
тате независимых решений установлены диапазоны значений параме-
тров
C
A
10
= 2
,
5
. . .
3
МПа,
C
A
01
= 0
. . .
0
,
45
МПа,
G
A
= 5
,
1
. . .
5
,
5
МПа,
λ
A
lock
= 1
,
5
. . .
1
,
7
.
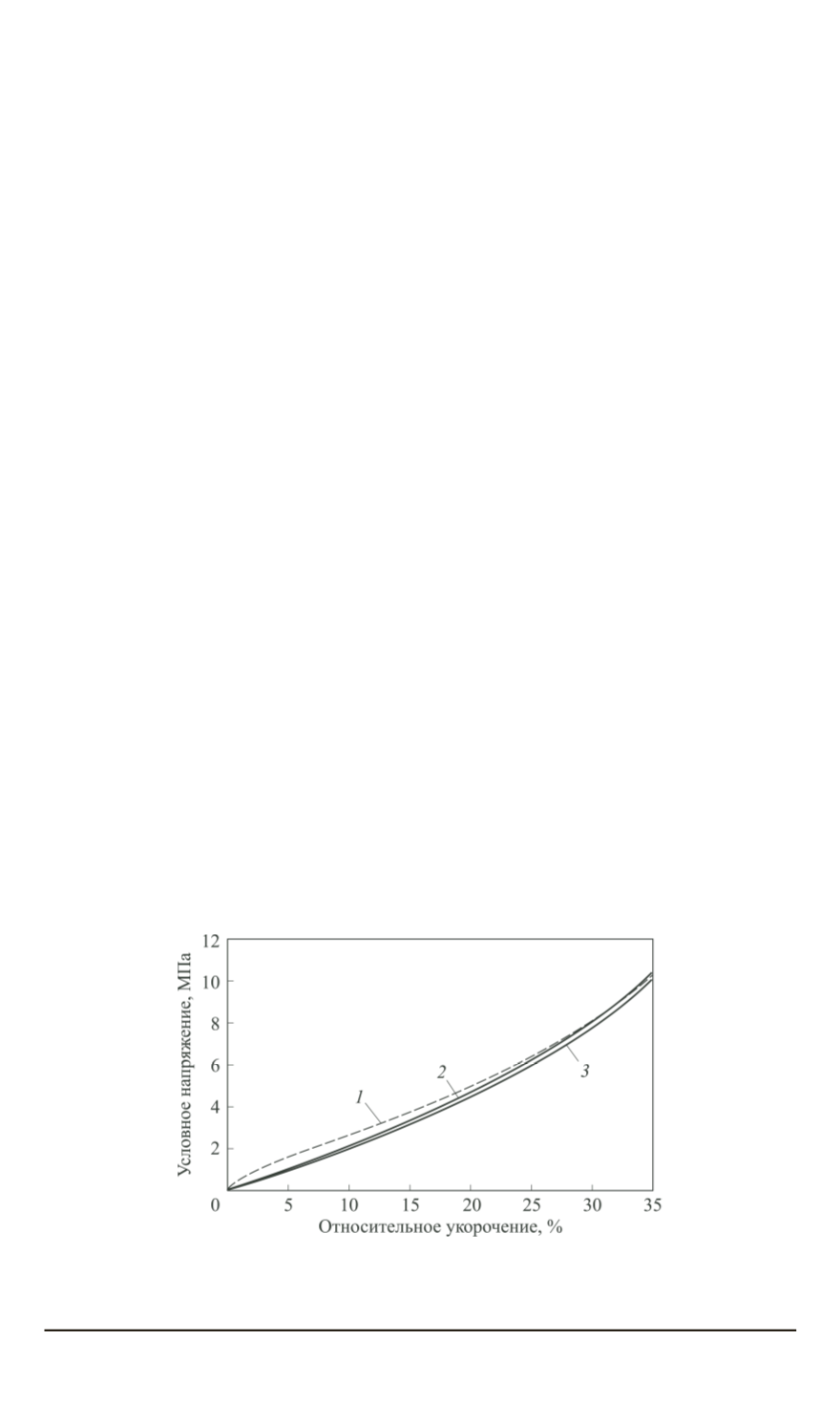
На рис. 5 показаны расчетные и экспериментальная статические
диаграммы сжатия полиуретана. Расчеты по модели Муни – Ривлина
выполнены при параметрах
C
A
10
= 3
МПа,
C
A
01
= 0
, по модели Арруда –
Бойс при
G
A
= 5
,
4
МПа,
λ
A
lock
= 1
,
65
. Видно, результаты моделирова-
ния (кривые
2
и
3
, см. рис. 5) мало различаются между собой. Поэто-
му при одноосном сжатии в рассмотренном диапазоне относительных
укорочений от 0 до 35% приемлемы обе модели. Подчеркивая при-
годность моделей в целом, отметим, что на начальном участке кривой
нагружения, где согласно результатам испытаний наблюдается сниже-
ние жесткости полиуретана, расчетные кривые несколько уклоняются
от экспериментальных (см. рис. 5).
В дальнейших расчетах упругих деформаций применялась модель
Муни – Ривлина.
Задача калибровки вязкоупругой модели Бергстрема – Бойс суще-
ственно сложнее, чем подбор коэффициентов для соотношений упру-
Рис. 5. Результат описания экспериментальной диаграммы сжатия полиуретана
(штриховая линия
1
) с помощью модели Муни – Ривлина (кривая
2
) и модели
Арруда – Бойс (кривая
3
)
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение” 2014. № 6 55


