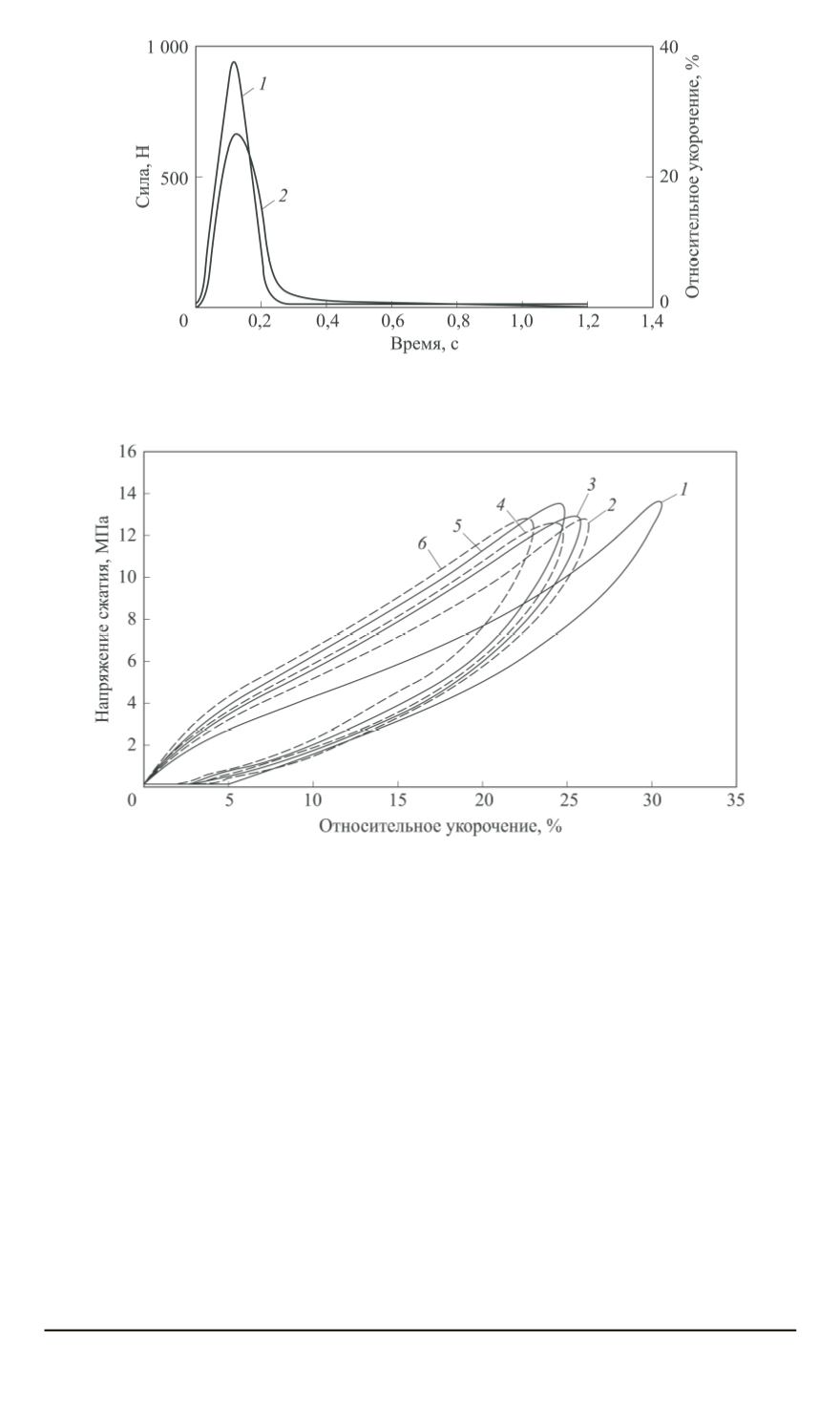
Рис. 2. Графики изменения во времени силы сжатия (кривая
1
) и относитель-
ного укорочения (кривая
2
) в течение одного цикла нагружения образца
Рис. 3. Диаграммы сжатия полиуретана СКУ-ПФЛ-100 при различных скоро-
стях нагружения и разгрузки:
1
— 13,5МПа/с;
2
— 135МПа/с;
3
— 338МПа/с;
4
— 474МПа/с;
5
— 677МПа/с;
6
—
812МПа/с
Характеристики гистерезисных потерь приведены в табл. 3.
Видно, что с ростом скорости нагружения в рассмотренном диапа-
зоне наблюдается некоторый рост относительного гистерезиса. Мини-
мальное значение гистерезиса наблюдается при статическом нагруже-
нии (см. табл. 1).
Представленные результаты положим в основу математического
описания поведения полиуретана.
Математическая модель поведения полиуретана.
Среди много-
численных предложений по формулировке законов вязкоупругости для
резиноподобных материалов одним из наиболее популярных являет-
ся предложение Бергстрема – Бойс [2]. Как показывают исследования
[2–4], модель Бергстрема – Бойс (в дальнейшем модель Б–Б) позволяет
48 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2014. № 6


