При
x
=
x
экс
=
l
d
2
˜
T
dx
2
= ˜
T
1
m
2
−
q
V
λ
с
1
ch (
ml
)
.
(34)
Отметим, что знак второй производной зависит от знака разности
в круглых скобках в правой части последнего выражения.
Представим разность температур
˜
T
1
−
˜
T
2
, используя формулу (33),
в виде
˜
T
1
−
˜
T
2
= ˜
T
1
m
2
−
q
V
λ
с
1
−
1
ch (
ml
)
1
m
2
,
(35)
где
1
−
1
ch (
ml
)
≥
0
.
Таким образом, если в формулах (34) и (35) выполняется условие
˜
T
1
m
2
−
q
V
λ
с
>
0
,
то в сечении стержня
x
=
l
˜
T
2
,
экс
= ˜
T
2
,
min
и
˜
T
1
>
˜
T
2
(
T
1
> T
2
)
.
В случае, когда
˜
T
1
m
2
−
q
V
λ
с
<
0
при
x
=
l
˜
T
2
,
экс
= ˜
T
2
,
max
и
˜
T
1
<
˜
T
2
(
T
1
< T
2
)
.
Зависимость температуры теплоизолированного с торца стержня от
координаты
x
для различных значений параметра
m
, иллюстрирующая
указанные замечания, представлена на рис. 2. Расчет выполнен для
значений
T
1
= 900
K;
T
с
= 300
K;
λ
с
= 200
Вт/(м
∙
K),
l
= 5
∙
10
−
3
м и
q
V
= 2
∙
10
8
Вт/м
3
. Выражения для тепловых потоков через основание,
торец и боковую поверхность стержня получаются из формул (27),
(28) и (30) соответственно, если принять в них Bi
2
= 0
. При этом
Q
2
≡
0
.
Анализ представленных на рис. 2 зависимостей распределения тем-
пературы по длине стержня позволяет выделить два характерных слу-
чая. В первом из них при отсутствии в стержне внутренних источников
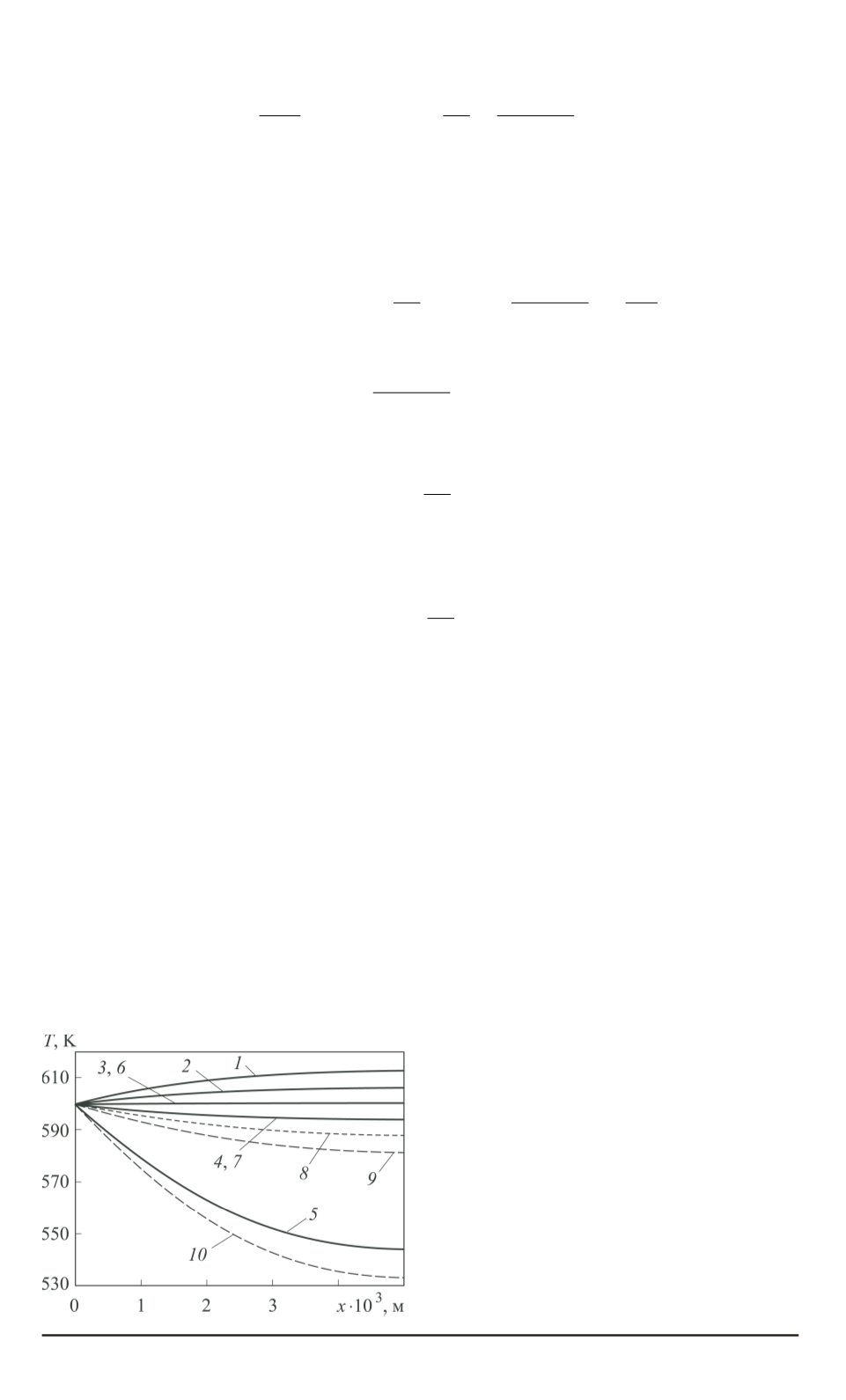
Рис. 2. Распределение температуры
по длине теплоизолированного с тор-
ца стержня
(
Bi
2
= 0)
:
кривые
1–5
соответствуют мощно-
сти внутренних источников теплоты
q
V
= 2
∙
10
8
Вт/м
3
и
m
= 1
, 30, 40,
50 и 100 соответственно; кривые
6–10
соответствуют тем же значениям чисел
m
при
q
V
= 0
36 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2014. № 2


