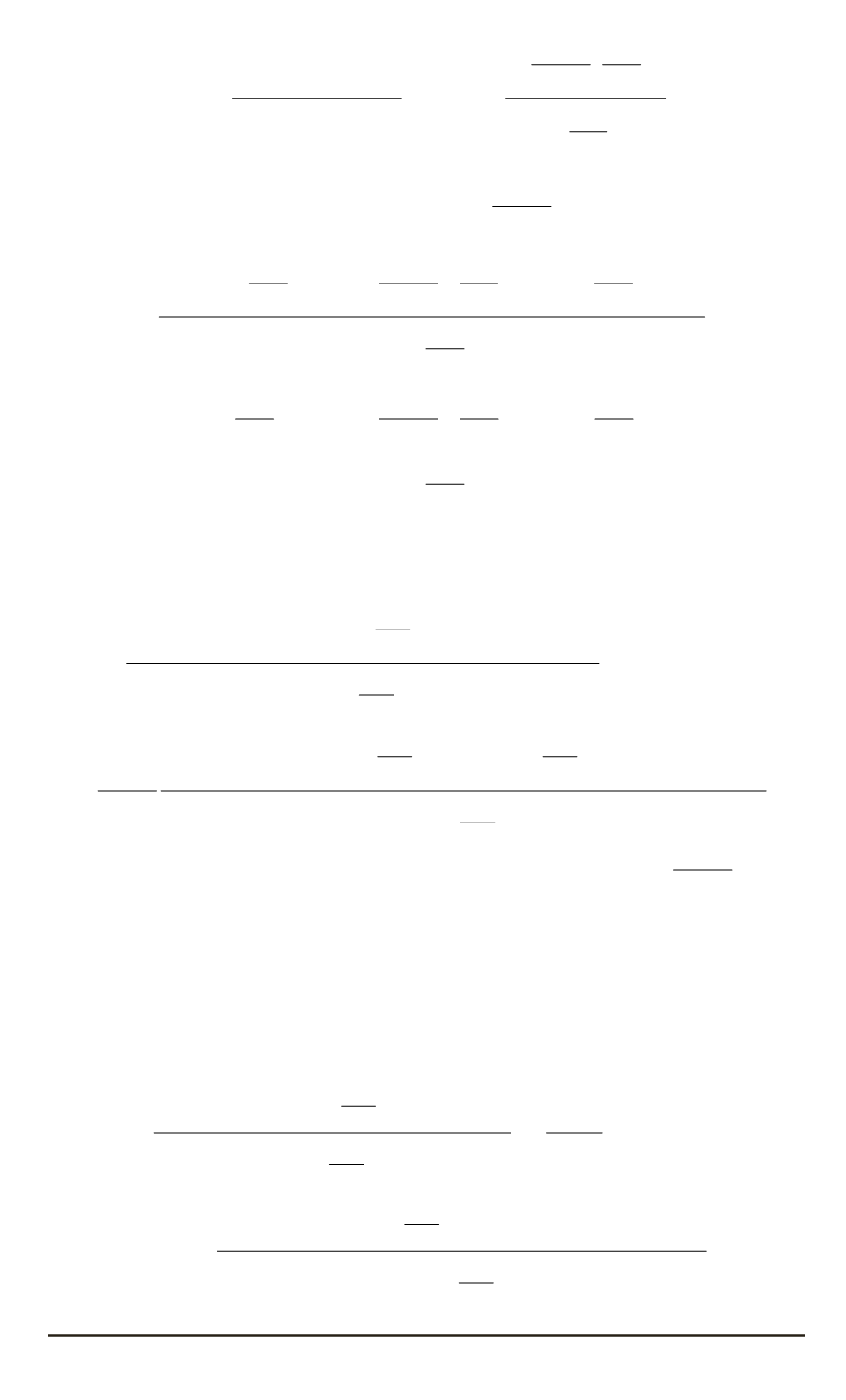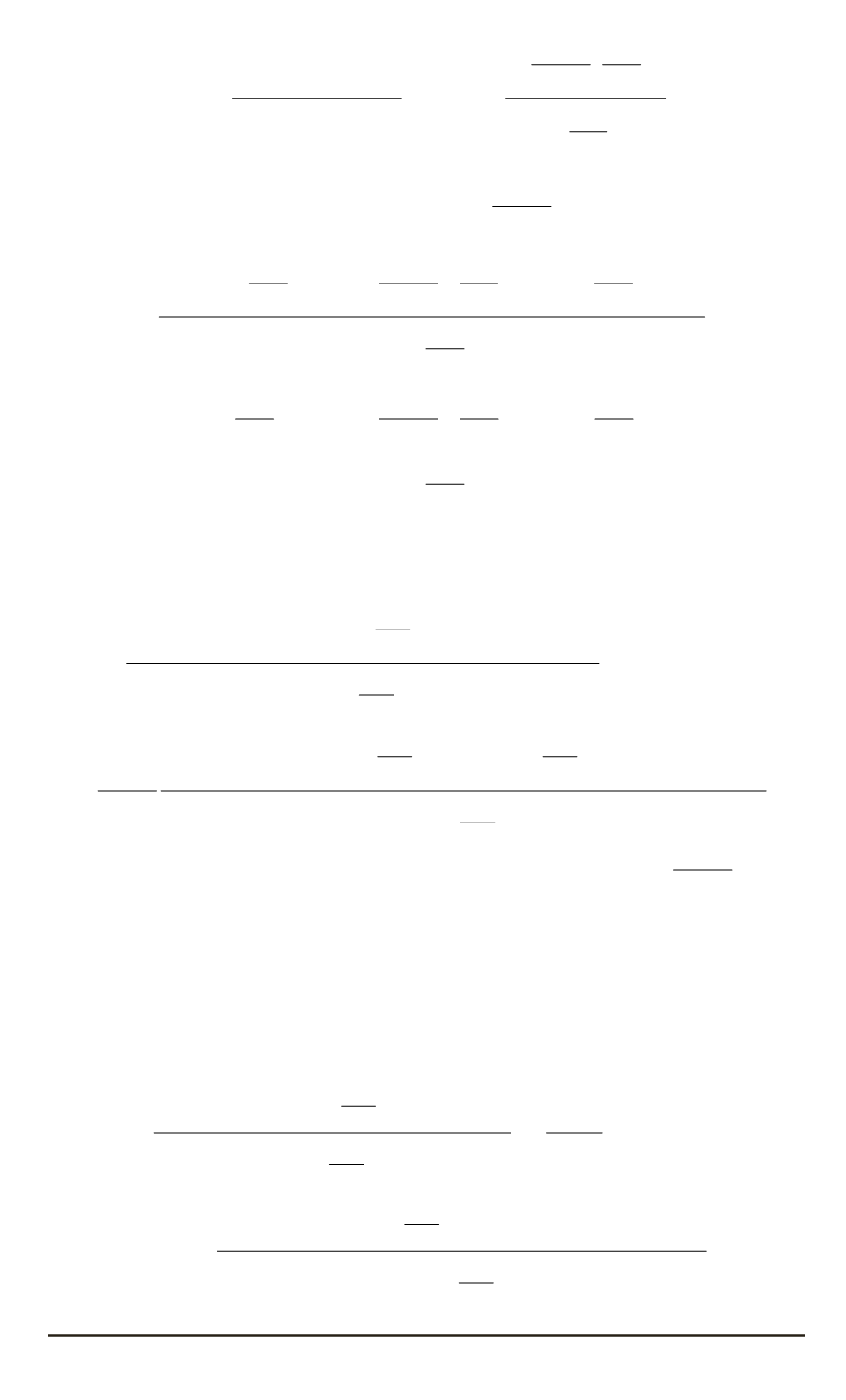
b
1
=
(
Bi
2
−
ml
)
e
−
ml
(
Bi
2
+
ml
)
e
ml
;
b
2
=
−
Po
(
ml
)
2
Bi
2
ml
1 +
Bi
2
ml
e
ml
;
b
3
= 1;
b
4
=
θ
1
−
Po
(
ml
)
2
;
C
3
=
θ
1
1 +
Bi
2
ml
e
ml
+
Po
(
ml
)
2
Bi
2
ml
−
1 +
Bi
2
ml
e
ml
(
e
ml
+
e
−
ml
) +
Bi
2
ml
(
e
ml
−
e
−
ml
)
;
(23)
C
4
=
θ
1
1
−
Bi
2
ml
e
−
ml
−
Po
(
ml
)
2
Bi
2
ml
+ 1
−
Bi
2
ml
e
−
ml
(
e
ml
+
e
−
ml
) +
Bi
2
ml
(
e
ml
−
e
−
ml
)
.
(24)
Подставляя постоянные интегрирования
C
3
и
C
4
из (23), (24), а
также выражения (22) в формулу (12), получаем
θ
=
θ
1
ch [
ml
(1
−
ξ
)] +
Bi
2
ml
sh [
ml
(1
−
ξ
)]
ch (
ml
) +
Bi
2
ml
sh(
ml
)
−
−
Po
(
ml
)
2
ch [
ml
(1
−
ξ
)] +
Bi
2
ml
sh (
mlξ
) +
Bi
2
ml
sh [
ml
(1
−
ξ
)]
ch (
ml
) +
Bi
2
ml
sh(
ml
)
+
+
Po
(
ml
)
2
.
(25)
После умножения левой и правой частей полученного решения на
T
m
,
формулу для расчета стационарного температурного поля стерж-
ня постоянного поперечного сечения с равномерно распределенными
в нем внутренними источниками теплоты можно представить в следу-
ющем виде:
˜
T
= ˜
T
1
ch [
m
(
l
−
x
)] +
Bi
2
ml
sh[m (
l
−
x) ]
ch (
ml
) +
Bi
2
ml
sh(
ml
)
+
q
V
λ
с
m
2
×
×
1
−
ch [
m
(
l
−
x
)] +
Bi
2
ml
{
sh (
mx
) +sh [
m
(
l
−
x)]
}
ch (
ml
) +
Bi
2
ml
sh(
ml
)
.
(26)
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение” 2014. № 2 33