Из сопоставления математической модели (6)–(8) с обобщенной
моделью (9)–(11) находим
a
ξξ
= 1;
b
ξ
= 0;
c
ξ
=
−
(
ml
)
2
;
F
(
ξ
) =
Po
=
const
;
γ
1
= 0;
γ
2
= 1;
β
1
= 1;
β
1
=
Bi
2
;
f
1
(
Fo
) =
θ
1
;
f
2
(
Fo
) = 0
.
(21)
Воспользовавшись таблицей, а также формулами (13)–(20)
получим
ψ
(
ξ
) = exp (
−
mlξ
) ;
ϕ
(
ξ
) = exp (
mlξ
) ;
H
1
(
ξ
) =
Po
2(
ml
)
2
e
mlξ
;
H
2
(
ξ
) =
Po
2 (
ml
)
2
e
−
mlξ
;
(22)
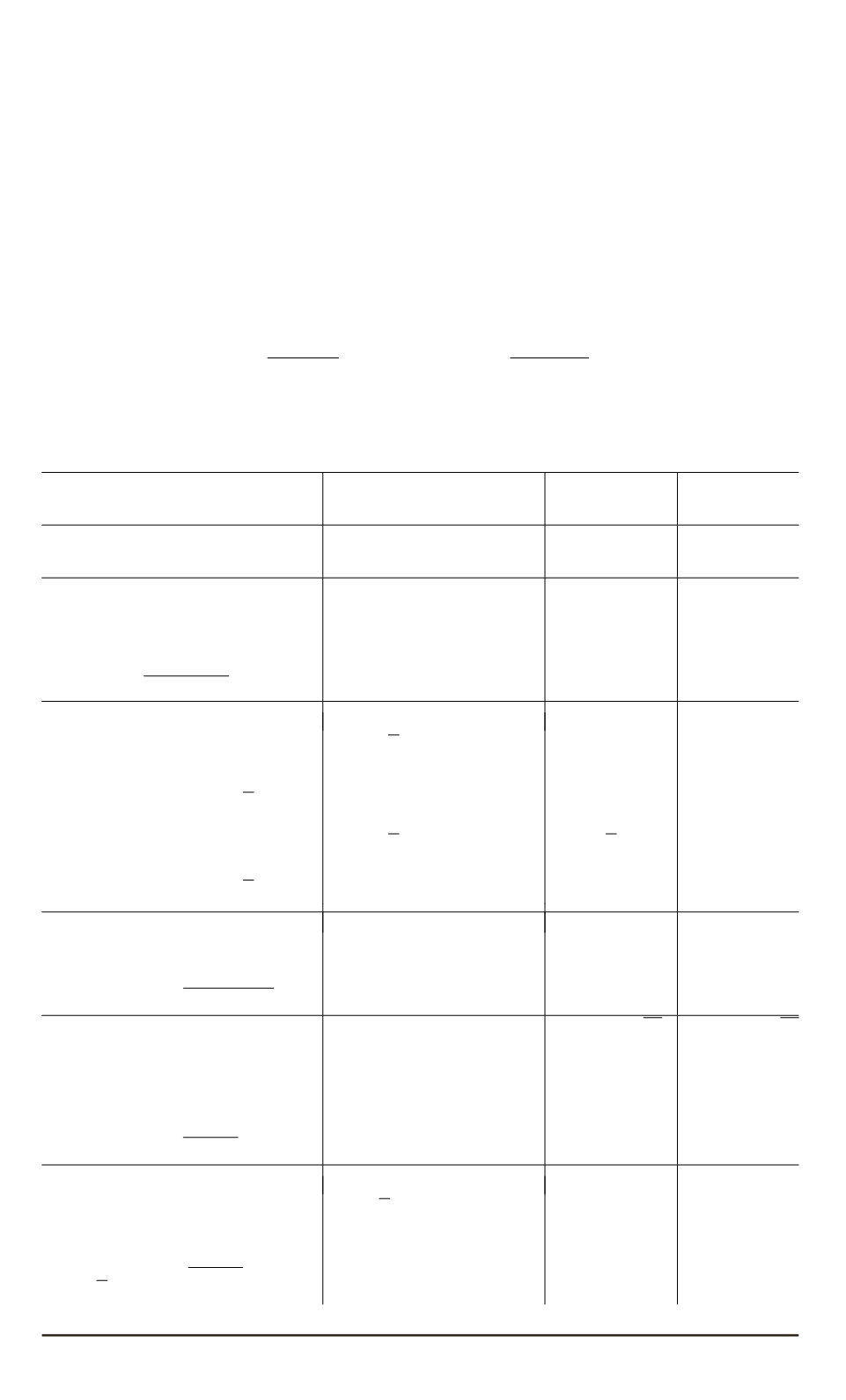
Математические модели для расчета температурного поля в телах простой
геометрической формы
Форма тела и коэффициенты
в уравнении (9)
Однородное уравнение
теплопроводности
Функция
ψ
(
ξ
)
Функция
ϕ
(
ξ
)
Пластина:
a
ξξ
= 1
,
b
ξ
=
c
ξ
= 0
θ
00
= 0
ξ
1
Пластина пористая, охлажда-
емая жидкостью:
a
ξξ
= 1
,
c
ξ
= 0
,
b
ξ
=
K
=
˙
mcl
λ
с
(1
−
p
)
θ
00
−
Kθ
0
= 0
exp(
Kξ
)
1
Цилиндр (сплошной или
полый):
a
ξξ
= 1
,
c
ξ
= 0
,
b
ξ
=
1
ξ
;
Шар (сплошной или полый):
a
ξξ
= 1
,
c
ξ
= 0
,
b
ξ
=
2
ξ
θ
00
+
1
ξ
θ
0
= 0
θ
00
+
2
ξ
θ
0
= 0
ln
ξ
1
ξ
1
1
Ребро (стержень) постоянно-
го сечения:
a
ξξ
= 1
,
c
ξ
=
−
(
ml
)
2
,
b
ξ
= 0
,
m
=
p
α
Π
/
(
λS
0
)
θ
00
−
(
ml
)
2
θ
= 0
exp(
−
mlξ
)
exp(
mlξ
)
Ребро треугольного и трапе-
циевидного поперечного се-
чения с малым углом при вер-
шине:
a
ξξ
= 1
, c
ξ
=
−
(
ml
)
2
,
b
ξ
= 1
,
m
=
p
α/λδ
)
ξθ
00
+
θ
0
−
(
ml
)
2
θ
= 0
I
0
(2
ml
p
ξ
)
K
0
(2
ml
p
ξ
)
Круглое ребро постоянной
толщины, равной
2
δ
:
a
ξξ
= 1
,
c
ξ
=
−
(
ml
)
2
,
b
ξ
=
1
ξ
,
m
=
p
α/λδ
)
θ
00
+
1
ξ
θ
0
−
(
ml
)
2
θ
= 0
I
0
(
mlξ
)
K
0
(
mlξ
)
32 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2014. № 2


