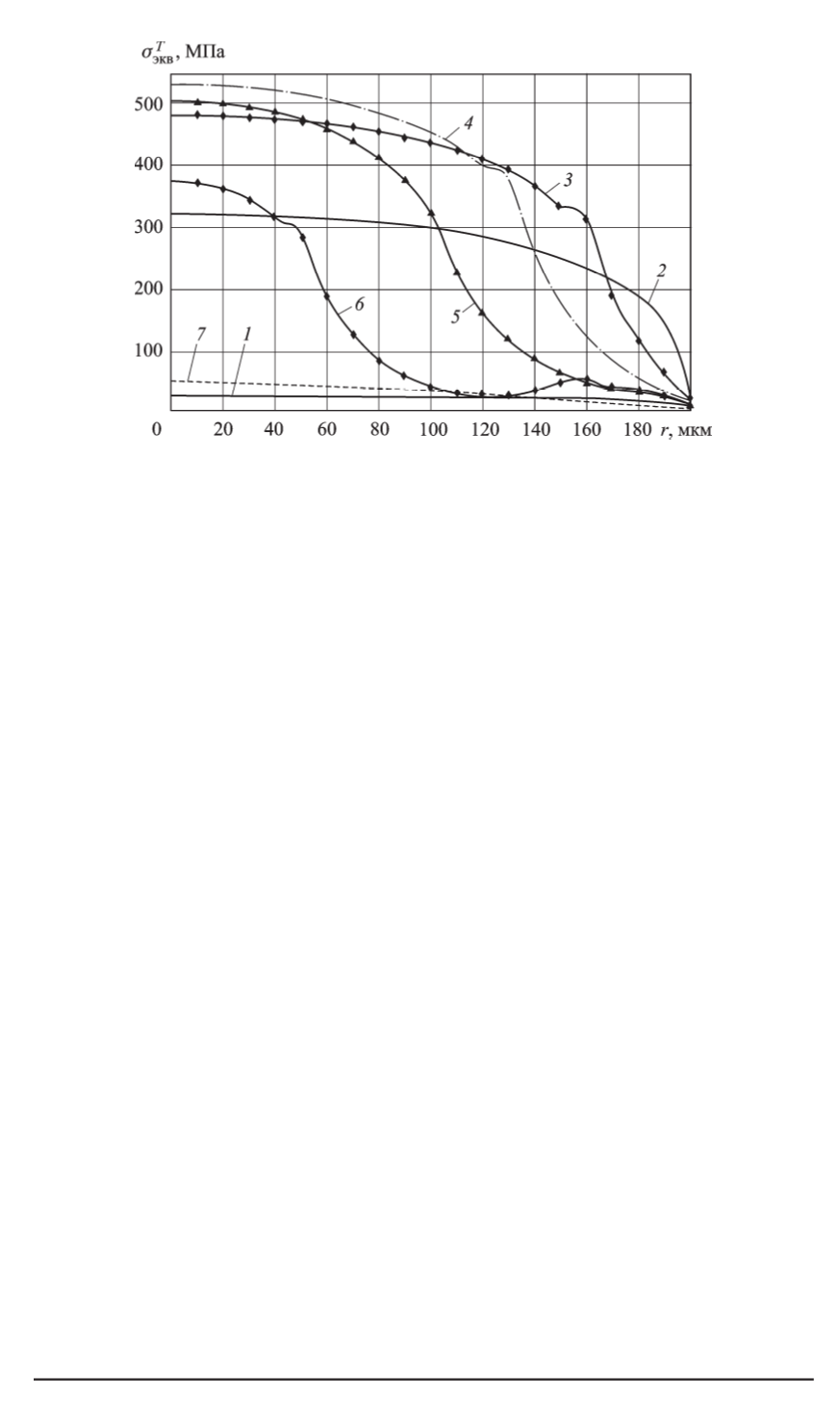
Рис. 5. Распределение эквивалентных термических напряжений по радиусу
частицы
d
= 0
,
4
мм при
T
m
= 1200
K в различные моменты времени:
1
—
t
= 0
,
1
t
p
;
2
—
t
= 0
,
9
t
p
;
3
—
t
= 1
,
6
t
p
;
4
—
t
= 2
,
3
t
p
;
5
—
t
= 3
t
p
;
6
—
t
= 3
,
8
t
p
;
7
—
t
= 10
t
p
стью аналогична приведенной выше. В момент времени
t
αβ
(опреде-
ляемый из соотношения
τ
αβ
=
t
αβ
/t
p
= ln[
T
m
/
(
T
m
−
Т
αβ
+
Т
0
)])
, когда
температура поверхности частицы достигает значения температуры
фазового перехода
Т
αβ
, ситуация существенно изменяется. По части-
це к ее центру начинаетдвигаться фронтфазового перехода, перед
которым кварц находится в
α
-фазе, а за которым — в
β
-фазе. Фазовый
переход происходитпри значительном изменении коэффициента объ-
емного расширения, что приводит к резкому увеличению эквивалент-
ных напряжений в центральной области частицы (занятой
α
-фазой) и
существенному их снижению во внешнем слое, представляющем со-
бой
β
-фазу кварца (рис. 5). В динамике это выглядит следующим обра-
зом: к центру частицы вместе с фронтом фазового перехода движется
фронтсвоеобразной “термодеформационной” волны (ТДВ), разграни-
чивающий области высоких и низких значений эквивалентных напря-
жений. По мере прохождения фронта фазового перехода по частице на
стадии роста общего температурного перепада
Δ ˜
T
в областях перед
фронтом ТДВ наблюдается рост
σ
T
экв
, максимальные значения дости-
гаются в момент времени
t
m
2
, когда фронтТДВ находится в точках
r
∼
d/
4
. Дальнейшее продвижение ТДВ к центру частицы сопровожда-
ется резким снижением значений
σ
T
экв
перед фронтом.
Характер изменения во времени
σ
T
экв
в центре частиц с различ-
ными диаметрами и при различных значениях
T
m
показан на рис. 6.
Временн´aя зависимость
σ
T
экв
(
r
= 0
, t
)
носитхарактер импульса коло-
колообразной формы длительностью, по порядку величины совпада-
ющей со временем прохождения фронтом фазового перехода (а сле-
довательно, ТДВ) тела частицы, т.е.
t
в
∼
d
2
/a
. Поэтому длительность
10 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2009. № 4


