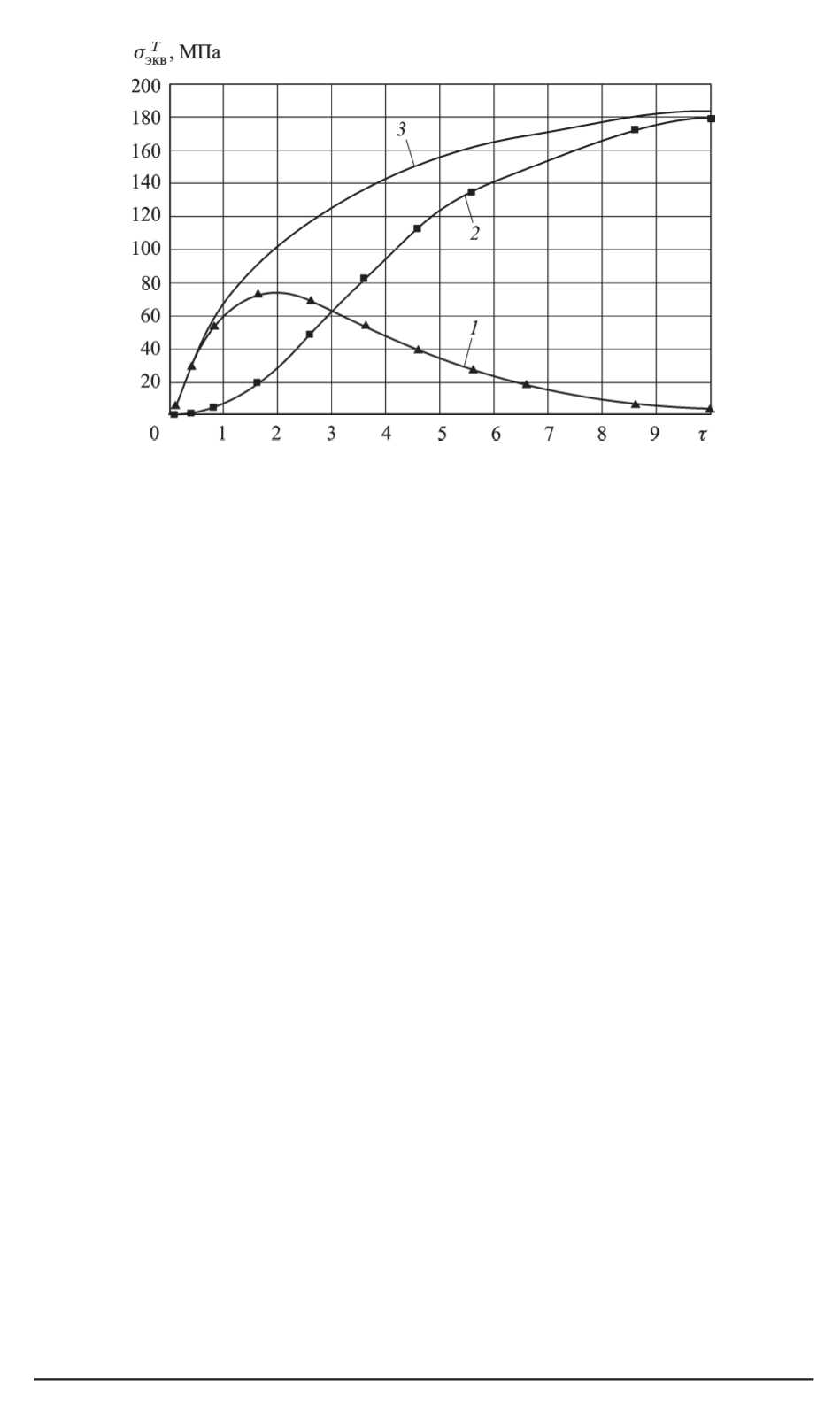
Рис. 9. Динамика эквивалентных термобарических напряжений на поверхно-
сти вакуоли для частицы
d
= 0
,
4
мм:
1
—
σ
T
экв
(
r
=
d
в
/2
, t
)
;
2
—
σ
P
экв
(
r
=
d
в
/2
, t
)
;
3
—
σ
TP
экв
(
r
=
d
в
/2
, t
)
барических напряжений
σ
TP
экв
и на снижение температуры разрушения
частицы.
На рис. 9 в качестве примера приведен расчетный график зависимо-
сти эквивалентного термобарического напряжения на поверхности ва-
куоли
σ
TP
экв
(
r
=
d
в
/2
, t
)
отвремени для кварцевой частицы
d
= 0
,
4
мм,
содержащей вакуоль
d
в
= 0
,
08
мм и заполненной жидким компонентом
(
Х
= 0
), при нагреве частицы с
T
m
= 200
K. Там же приведены графи-
ки зависимостей от
t
отдельных составляющих эквивалентного термо-
барического напряжения: термического
σ
T
экв
(
r
=
d
в
/2
, t
)
и барического
σ
P
экв
(
r
=
d
в
/2
, t
)
. Видно, что на начальной фазе нагрева (
t
≈
0
. . .
3
t
p
)
,
когда температура ГЖВ относительно мала, термические напряжения
превышают барические. После прогрева центральной области части-
цы с ГЖВ барические напряжения становятся преобладающими. При
этом полные термобарические напряжения
σ
TP
экв
являются монотонно
возрастающими функциями времени. В данном случае максимальные
значения термического напряжения в частице не достигают предельно-
го значения
σ
вр
. Частица разрушается под действием термобарическо-
го напряжения, значение которого начинает превышать допустимый
порог
σ
вр
в моментвремени
≈
2
t
P
.
Значение давления ГЖВ, при котором максимальные барические
напряжения
σ
P
экв
(
r
=
d
в
/2
, t
)
превышаютдопустимый порог
σ
вр
и ча-
стица с вакуолью будет разрушена, определяется по уравнению (7) и
составляет для кварцевой частицы
Р
разр
≈
2
σ
вр
≈
10
2
МПа. Установлен-
ная зависимость
P
=
P
¯
T , X
позволяет рассчитать (см. рис. 8) тем-
пературу
T
P
разр
(
X
)
, при которой давление ГЖВ достигает значения
Р
разр
. Величина
T
P
разр
(
Х
)
представляет собой температуру чисто бари-
16 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2009. № 4


