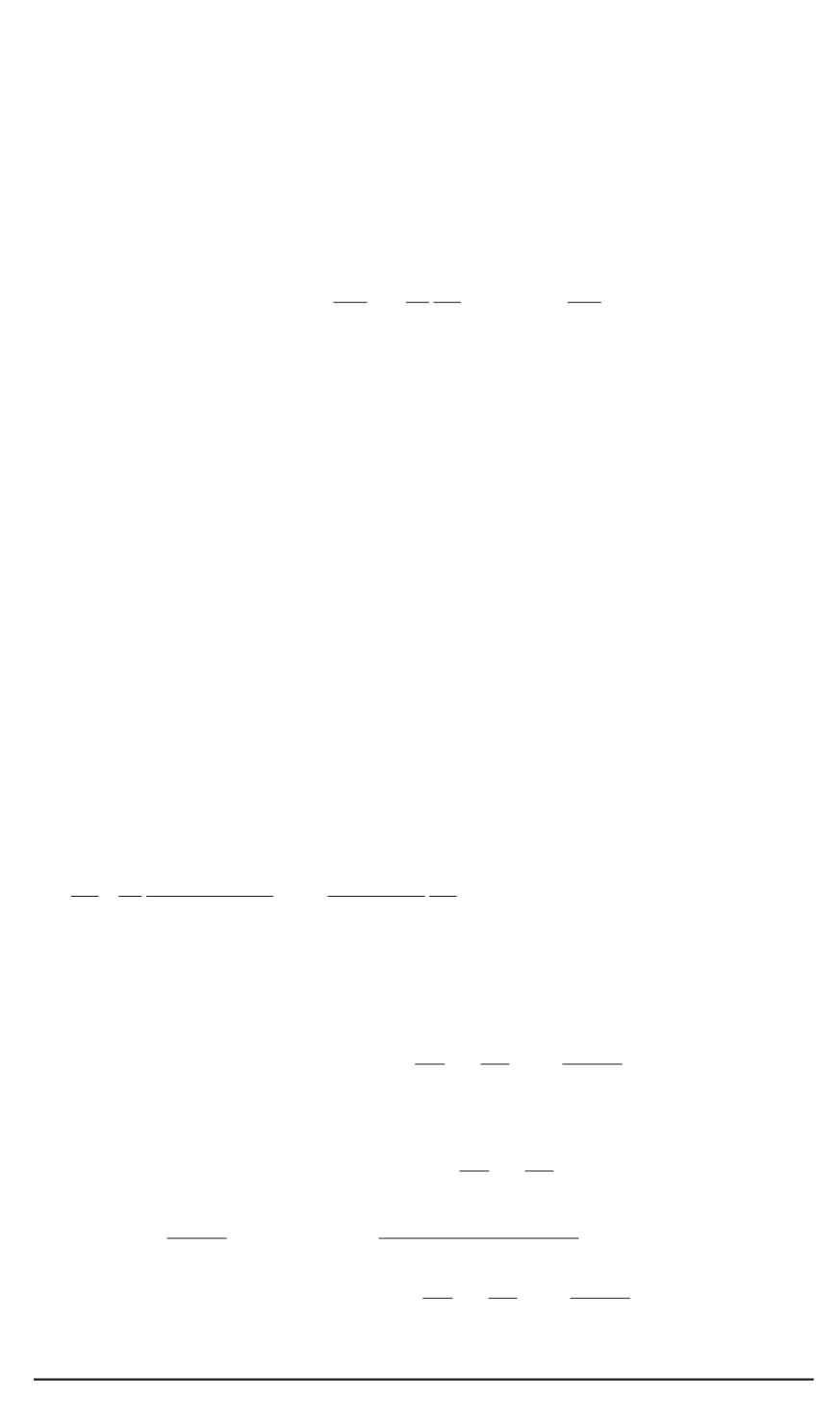
Поскольку теплота фазового перехода
α
–
β
-кварц
Δ
Н
αβ
= 1
,
8
×
×
10
−
2
Дж/кг [3] существенно меньше значения удельной энтальпии
кварца при температуре
Т
αβ
, то при расчете температурного поля ча-
стицы можно пренебречь влиянием фазового перехода, т.е. задачу фор-
мулировать не как задачу Стефана, а как обычную задачу нестационар-
ной теплопроводности, описываемую дифференциальным уравнением
Фурье–Кирхгофа в сферических координатах:
ρ
(
T
)
C
p
(
T
)
∂T
∂t
=
1
r
2
∂
∂r
λ
(
Т
)
r
2
∂T
∂r
.
(3)
В отсутствие вакуоли уравнение (3) решается в области
r
∈
(0
, d/
2)
,
а при наличии вакуоли — в области
r
∈
(
d
в
/
2
, d/
2)
.
Начальные и граничные условия для уравнения (3) следующие:
t
= 0
, T
=
T
0
= 300
K
;
T
(
r
=
d/
2
, t
) =
T
s
(
t
);
∂T/∂r
r
=0
= 0
— для частицы без вaкуоли
;
∂T/∂r
r
=
d
в
/
2
= 0
— для частицы c вaкуолью
.
(4)
Последнее выражение записано в предположении, что температура
ГЖВ в вакуоли в среднем по объему одинакова и равна температуре
поверхности вакуоли. Компоненты тензора напряжений в кварцевой
частице
σ
rr
,
σ
ϕϕ
,
σ
θθ
, главные (
σ
1
,
σ
3
) и эквивалентные (
σ
экв
) напря-
жения определялись на основе результатов численного решения со-
ответствующего уравнения равновесия [5], записанного относительно
вектора смещения
u
, имеющего в условиях сферической симметрии
только радиальную компоненту
u
(
r
)
,
∂
∂r
1
r
2
∂r
2
(
u
(
r, t
))
∂r
=
1 +
σ
3 (1
−
σ
)
∂
∂r
α
(
T
(
r, t
))(
T
(
r, t
)
−
T
0
)
,
(5)
где
α
(
T
(
r, t
))
— коэффициентобъемного расширения.
Уравнение (5) решали со следующими краевыми условиями:
r
= 0
,
u
= 0
,
r
=
d/
2
, σ
rr
= 0
или
(1
−
σ
)
∂u
∂r
+
4
σ
d
u
=
1 +
σ
3
α
(
T
−
T
0
)
(6)
— для частицы без вакуоли;
r
=
d
в
/
2
, σ
rr
=
−
Р
или
(1
−
σ
)
∂u
∂r
+
4
σ
d
в
u
=
=
1 +
σ
3
α
(
T
−
T
0
)
−
P
(1 +
σ
) (1
−
2
σ
)
E
,
r
=
d/
2
, σ
rr
= 0
или
(1
−
σ
)
∂u
∂r
+
4
σ
d
u
=
1 +
σ
3
α
(
T
−
T
0
)
(7)
— для частицы с вакуолью.
6 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2009. № 4


