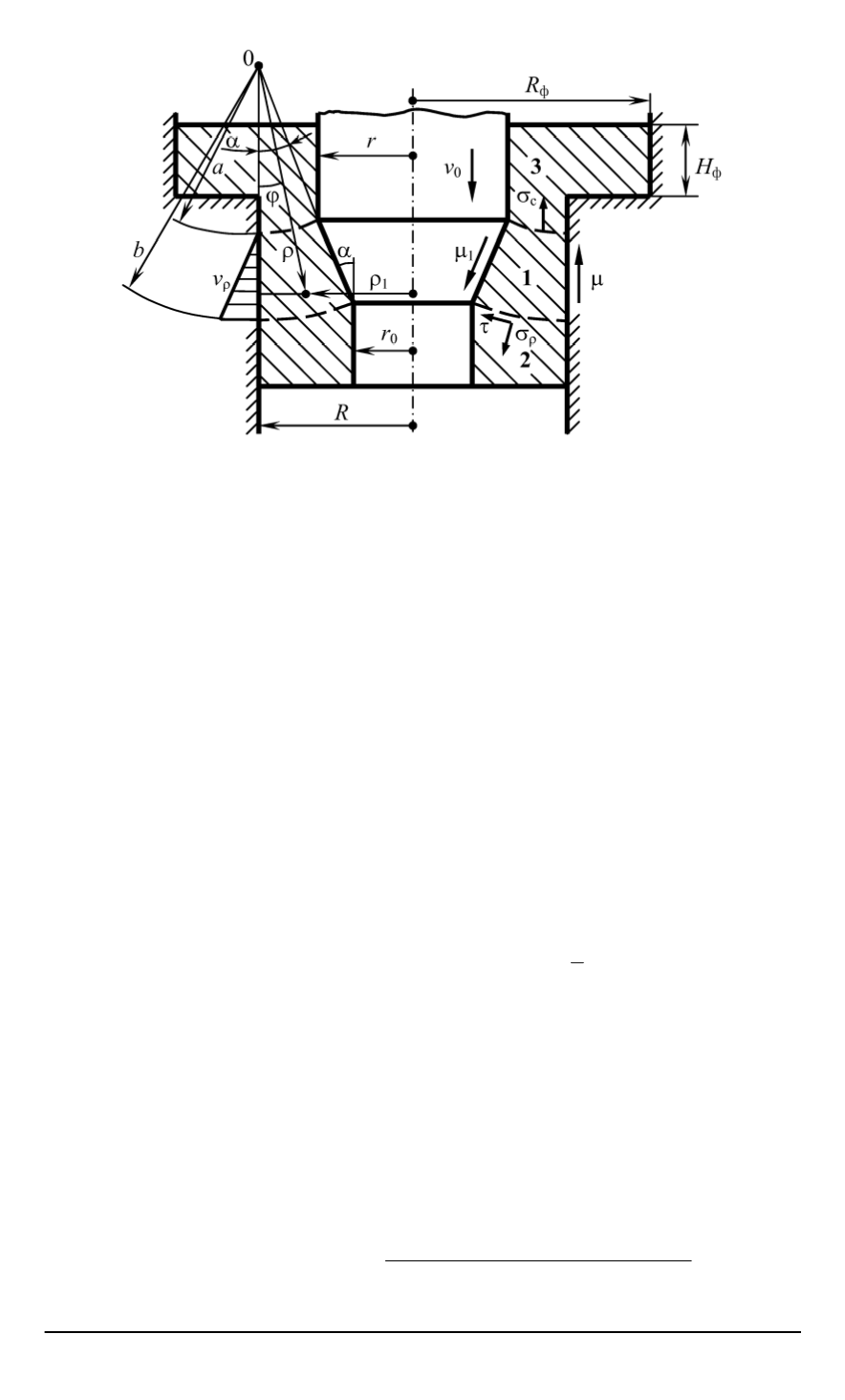
Рис. 6. Расчетная схема вытяжки по внутренней поверхности
предельных касательных напряжений
τ
= 0
,
5
β
. Аналогичные усло-
вия имеют место и на границе между зонами
1
и
3
. С учетом этого
произвольную постоянную
С
2
определяем из следующего граничного
условия:
π
(
R
2
−
r
2
0
)
σ
ρ
|
ρ
=
b
−
P
τ
|
ρ
=
b
= 0
.
(7)
Первое выражение этого уравнения написано с учетом известной те-
оремы [10] об определении силы в зависимости от напряжения, пере-
менного по направлению, но постоянного по величине.
Сила от действия касательных напряжений
τ
= 0
,
5
β
равна
P
τ
|
ρ
=
b
= 2
π
R
Z
r
0
τ
sin
ϕρ
1
dρ
1
=2
π
α
Z
0
τ
sin
ϕ
(
R
−
b
sin
ϕ
)
bdϕ
=
=
πβb R
(1
−
cos
α
)
−
b
4
(2
α
−
sin 2
α
)
.
(8)
Для облегчения практических расчетов радианное значение угла
α
в выражениях (6) и (8) в силу малости заменим на
sin
α
. В результате
получаем
P
τ
|
ρ
=
b
=
πβb
(1
−
cos
α
)(
R
−
0
,
5
b
sin
α
)
.
(9)
Подставив выражение (9) в уравнение (7), найдем произвольную
постоянную
C
2
=
−
β
−
(
C
−
β
) ln
b
+
βb
(1
−
cos
α
)(
R
−
0
,
5
b
sin
α
)
R
2
−
r
2
0
.
(10)
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2011. № 2 93


