Метод расчета сверхзвукового обтекания сферы на основе AUSM конечно-разностных схем - page 17

а остальные коэффициенты (C i,j, F i,j) и функции — такие же, как в
схеме Т-1. В заключение изложения различных модификаций конечно -раз- ностной схемы заметим , что результаты численных расчетов , пред- ставленные в настоящей работе , получены с использованием схемы
T-1 для решения уравнения сохранения энергии, которая оказалась
наиболее эффективной в рассматриваемых условиях, а также AUSM конечно-разностной схемы для решения уравнений движения без до - полнительной модификации численных решений. Результаты численного моделирования. Разработанный метод
тестировался сравнением с результатами расчета параметров ударного
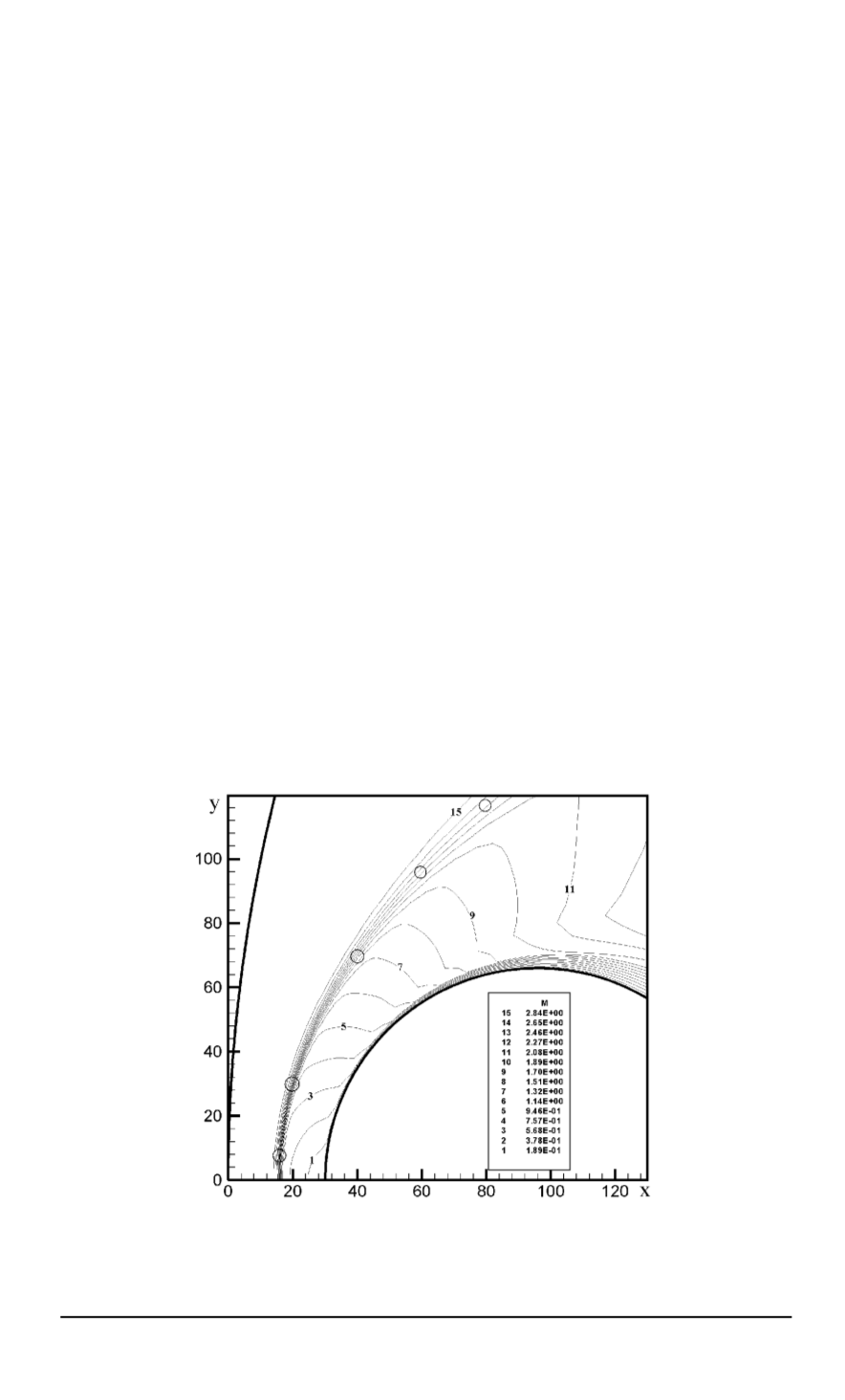
слоя у сферы, обтекаемой сверхзвуковым потоком , представленны - ми в работах [4, 10]. В качестве примера такого сравнения на рис. 2 показано распределение чисел Маха у поверхности сферы радиусом
R = 66 см вязким теплопроводным совершенным газом с показателем
адиабаты γ = 1 ,4 при следующих исходных данных: p∞ = 7, 6 эрг/см3 ,
ρ ∞ = 2, 82 ∙ 10−8 г/см3 , MΣ = 29 г/моль, T∞ = 297 K, V∞ = 1 ,035 ×
× 105 см/с. Приведенные данные отвечают одной из наиболее грубых
из использованных расчетных сеток (NI = 55 × NJ = 101, где NI — число узлов по нормальной к поверхности переменной (η)). Поэтому
точность расчетов газодинамических функций у обтекаемой сферы , в особенности вблизи боковой и задней поверхности , является здесь
весьма низкой . Тем не менее , приведенные на рис. 2 данные свидетель-
Рис . 2. Изолинии числа Маха при M = 3, γ = 1 ,4 вблизи поверхности сферы; кружками показаны результаты расчета [10] для положения ударной волны; x и
y в см
ISSN 0236-3941. Вестник МГТУ им. Н .Э. Баумана . Сер . “Машиностроение”. 2005. № 3 23