и сдвиге
;
I
и
F
—
момент инерции и площадь сечения
;
R
ф
—
внешняя
фиктивная сила
;
k
—
безразмерный коэффициент
,
зависящий от формы
сечения
;
z
—
текущая координата по длине валка с нулевой точкой в
месте приложения силы
R
ф
;
a
—
расстояние между опорами валка
.
Фиктивную силу
R
ф
,
согласно теореме
,
прикладывают в месте
определения прогиба и направляют по направлению деформации
.
Задачу межвалкового контакта решали на основе гипотезы Винкле
-
ра
,
согласно которой контактная деформация в любой точке контакта
y
kw
=
K
kw
q
kw
,
(9)
где
K
kw
—
коэффициент податливости упругого основания
;
q
kw
—
по
-
гонная нагрузка в межвалковом контакте
;
w
—
текущая координата на
длине бочки
(
см
.
рис
. 2).
Для определения коэффициента
K
kw
была использована формула
Б
.
С
.
Ковальского
[7].
Для вывода формул прогибов валковой системы были приняты сле
-
дующие допущения
:
распределение межвалкового контактного усилия
подчиняется параболическому закону
(
парабола второго порядка
);
уси
-
лие прокатки по ширине листа распределяется равномерно
;
влияние
сил трения в межвалковом контакте пренебрежительно мало
;
валки из
-
готовлены монолитными
(
без бандажей
).
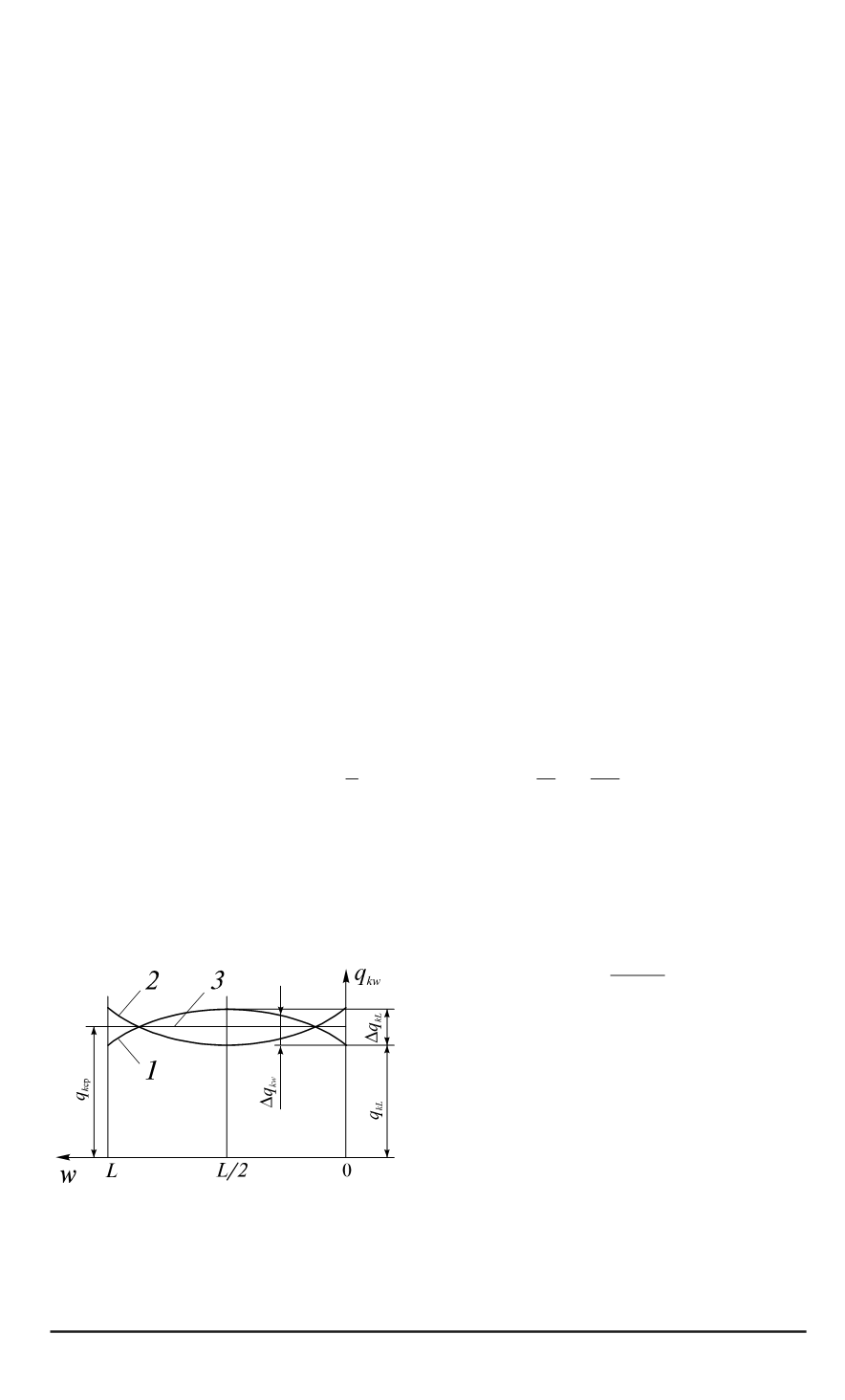
В соответствии с первым допущением получим
q
kw
=
q
k
ср
−
2
3
∆
q
kL
+ 4∆
q
kL
s
w
L
−
w
2
L
2
t
.
(10)
Обозначения величин в выражении
(10)
ясны из рис
. 3.
Для характеристики неравномерности распределения межвалково
-
го усилия был введен коэффициент неравномерности распределения
Рис
. 3.
Диаграмма распределения
межвалкового контактного усилия
по длине бочки
;
1, 2, 3
—
возможные
варианты распределения
λ
=
∆
q
kL
q
k
ср
,
где
∆
q
kL
=
q
k
c
−
q
kL
(
q
k
c
,
q
kL
—
по
-
гонные силы по середине и у края
бочки
).
В зависимости от распределе
-
ния погонной силы по длине боч
-
ки величина
∆
q
kL
может быть по
-
ложительной или отрицательной
.
В
связи с этим и коэффициент
λ
мо
-
жет иметь разный знак
.
84 ISSN 0236-3941.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. “
Машиностроение
”. 2004.
№
4


