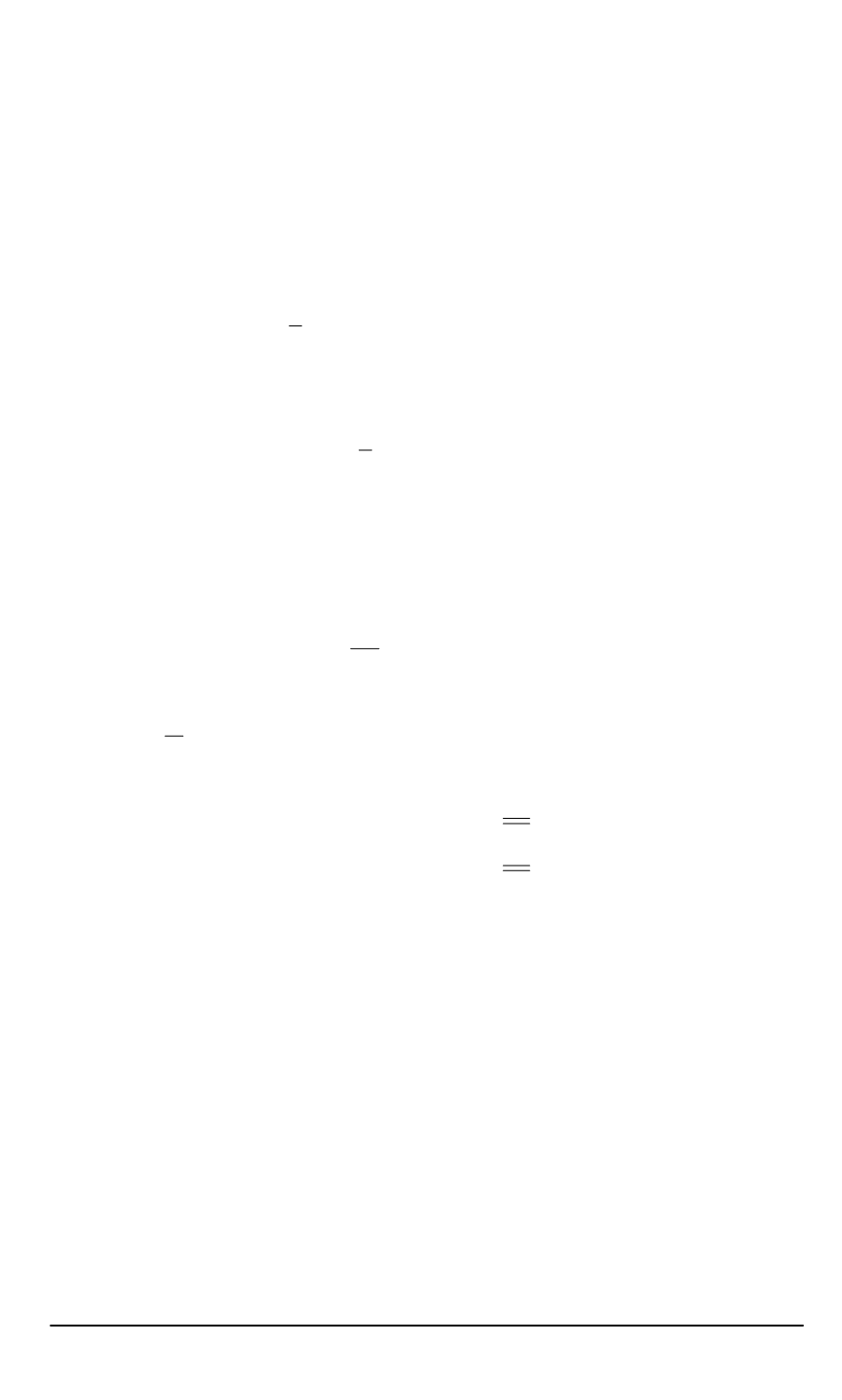
И равенство
(9)
можно переписать в виде
z
s j
=
z
0
+
k
0 0 1
k ·
°°°°°°
0
−
γ
α
γ
0
−
β
−
α
β
0
°°°°°°
·
°°°°°°
ξ
s j
η
s j
ζ
s j
°°°°°°
=
z
0
−
αξ
s j
+
βη
s j
.
Подставляя последнее равенство в выражение для потенциальной
энергии подвески
,
получим
Π
п
=
1
2
2
n
o
∑
j
=
1
C
п
j
(
z
j
−
z
0
+
αξ
s j
−
βη
s j
)
2
.
Далее
Π
ш
=
1
2
2
n
o
∑
j
=
1
C
ш
j
(
z
д
j
−
z
j
)
2
,
здесь
C
ш
j
—
коэффициент нормальной
(
радиальной
)
жесткости шины
j
-
го колеса
;
z
д
j
—
вертикальная координата дороги под центром
j
-
го
колеса
—
под точкой
O
j
,
z
д
j
=
h
д
sin
·
2
π
L
д
(
x
д
j
cos
ϕ
д
+
y
д
j
sin
ϕ
д
)
¸
,
где
x
д
j
и
y
д
j
—
продольная и поперечная координаты точки
O
j
в системе
координат
OXYZ
.
В первом приближении
,
по аналогии с выражением
(7),
получим
x
д
j
=
x
0
+
k
1 0 0
k
r
∗
s j
;
y
д
j
=
y
0
+
k
0 1 0
k
r
∗
s j
или с учетом равенств
(8)
и
(10)
x
д
j
=
x
0
+
k
1 0 0
k ·
°°°°°°
1
−
γ
α
γ
1
−
β
−
α
β
1
°°°°°°
·
°°°°°°
ξ
s j
η
s j
ζ
s j
°°°°°°
=
x
0
+
ξ
s j
−
γη
s j
+
αζ
s j
;
y
д
j
=
y
0
+
k
γ
1
−
β
k ·
°°°°°°
ξ
s j
η
s j
ζ
s j
°°°°°°
=
y
0
+
γξ
s j
+
η
s j
−
β ζ
s j
.
Таким образом
,
выражение для потенциальной энергии шины явля
-
ется существенно нелинейным
,
в котором в качестве аргументов у си
-
нуса присутствуют обобщенные координаты
x
0
,
y
0
,
α
,
β
,
γ
.
22 ISSN 0236-3941.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. "
Машиностроение
". 2003.
№
4