dy
1
dη
=
y
2
A
11
;
dy
2
dη
=
A
33
Ω
30
Ω
3
sin
y
1
,
(11)
где
y
1
=
ϑ
(
/
)
1
, y
2
=
M
1
.
Рассмотрим режим вращения вала, когда при
η
= 1
M
1
k
= 0
. Для
того чтобы получить решение, удовлетворяющее этому условию, при-
ходится, задавая угол
ϑ
(
/
)
10
и изменяя
M
10
, при помощи численного
решения системы уравнений (11) определять такое значение
M
10
, при
котором при
η
= 1
M
1
(
η
) = 0
. При численном решении системы
уравнений (11) брались следующие числовые значения размерных па-
раметров:
d
= 5
∙
10
−
3
м
, l
= 1
м
,
l
=
1
3
πR
;
e
A
33
=
e
A
22
=
E
πd
4
64
= 6
,
443
Н
∙
м
2
,
e
A
11
=
GJ
k
=
E
2 (1 +
μ
)
πd
4
32
= 5
,
113
Н
∙
м
2
,
E
= 2
,
1
∙
10
11
Па
, μ
= 0
,
26
,
e
Ω
3
=
1
R
=
const
,
e
Ω
30
=
1
R
0
=
const
(
R, R
0
— радиусы кривизн канала и стержня).
Безразмерные параметры, входящие в уравнения (11), можно
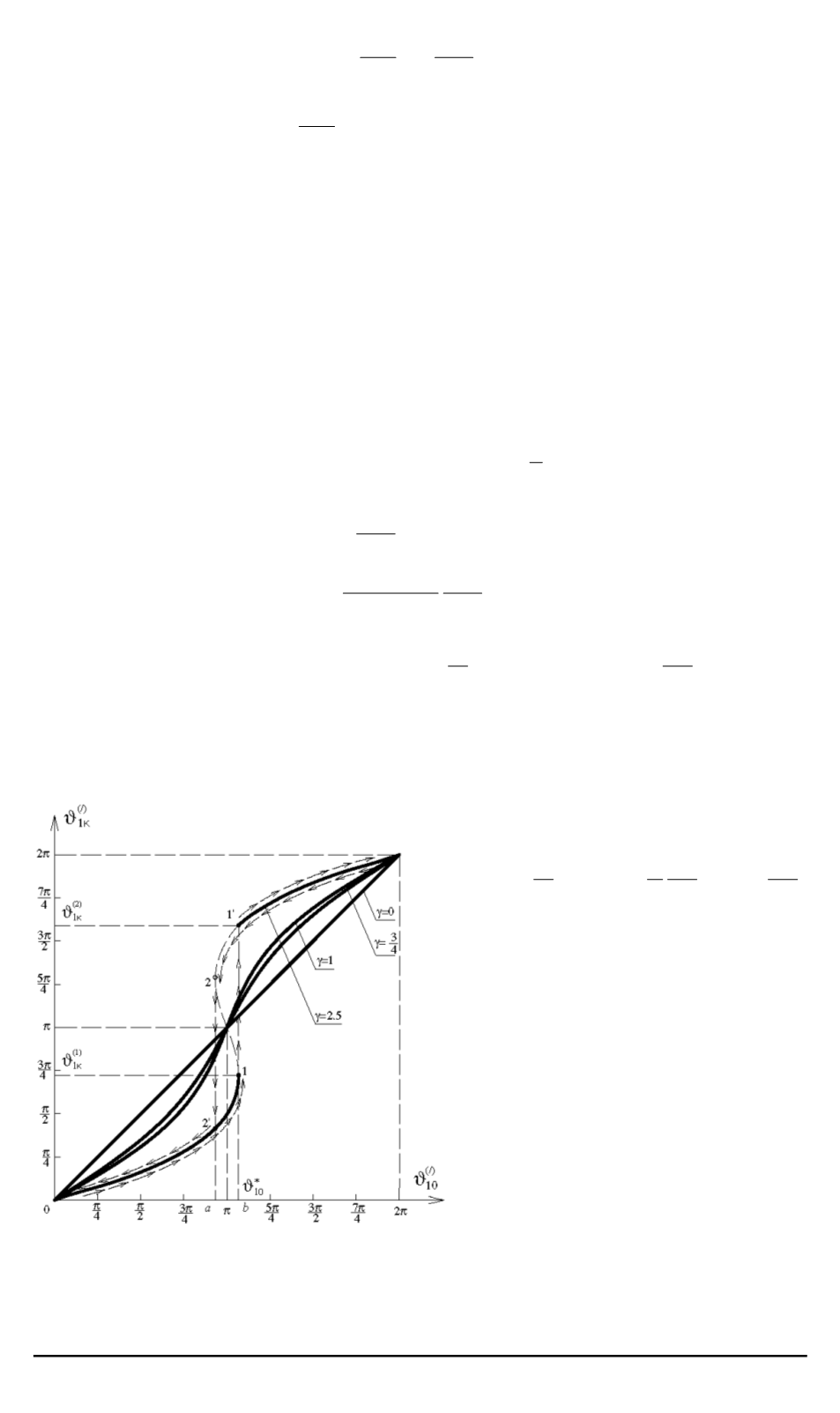
Рис. 2. Графики зависимости угла
ϑ
1к
от
угла
ϑ
10
представить как
A
22
=
A
33
= 1
, A
11
= 0
,
7937
,
Ω
3
=
π
R
,
Ω
30
=
π
3
R
R
0
, γ
=
R
R
0
.
Результаты численного ре-
шения системы уравнений (11)
приведены на рис. 2–7. На
рис. 2 приведен график зави-
симости
ϑ
(
/
)
1
k
ϑ
(
/
)
10
для раз-
ных значений параметра
γ
.
При значениях
γ
из интерва-
ла
0
≤
γ
6
1
,
2
имеет место
однозначная зависимость
ϑ
(
/
)
1
k
от
ϑ
(
/
)
10
, т.е. при непрерывном
изменении угла
ϑ
(
/
)
10
угол
ϑ
(
/
)
1
k
изменяется также непрерывно.
При
γ
≥
1
,
2
(например, при
100 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2006. № 3


