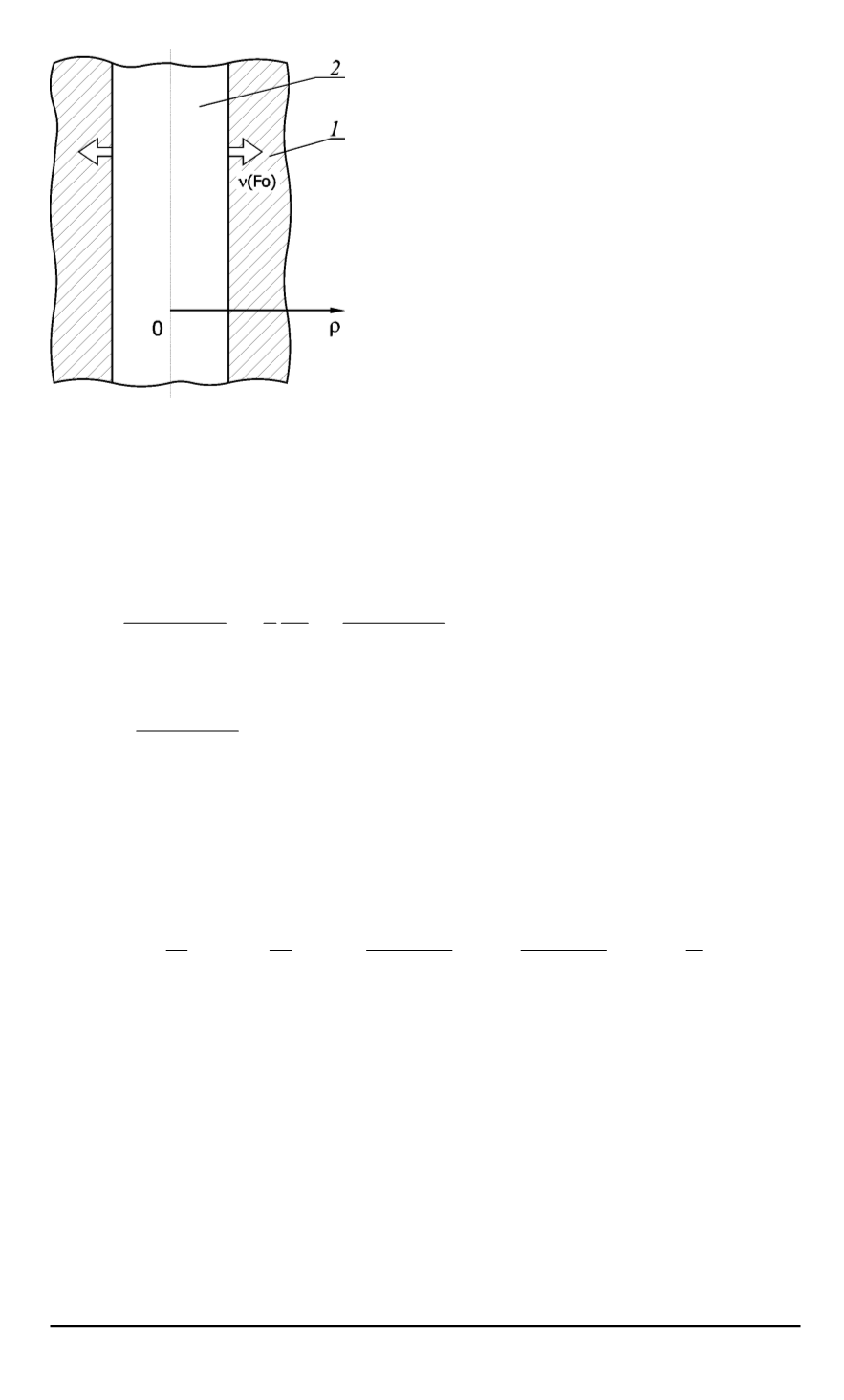
Рис. 1. Используемая расчетная
схема:
1
— твердое тело,
2
— внешняя
среда
твердом изотропном теле с цилиндри-
ческим каналом (рис. 1), заполненным
высокотемпературным газом (в дальней-
шем — внешней средой), граница кото-
рого движется по заданному закону
ν
(
Fo
) = 1 +
ε
Fo
,
(1)
где
ε
— малый положительный параметр.
При этом предполагается, что процесс
теплообмена с внешней средой сопро-
вождается временн ´ым изменением ко-
эффициента теплоотдачи на подвижной
границе цилиндрического канала, т. е.
является нестационарным.
Постановка задачи.
В соответствии
с поставленной целью и с учетом допу-
щения (1) исходная математическая модель исследуемого процесса
имеет вид
∂
Θ(
ρ,
Fo
)
∂
Fo
=
1
ρ
∂
∂ρ
ρ
∂
Θ(
ρ,
Fo
)
∂ρ
;
Fo
>
0
, ρ > ν
(
Fo
)
>
1
,
Θ(
ρ,
Fo
)
Fo
=0
= 0
,
(2)
ρ
∂
Θ(
ρ,
Fo
)
∂ρ
ρ
=
ν
(
Fo
)
=
Bi
(
Fo
)
h
Θ(
ρ,
Fo
)
ρ
=
ν
(
Fo
)
−
ζ
(
Fo
)
i
,
Θ(
ρ,
Fo
)
Fo
>
0
2
L
2
[
ν
(
Fo
)
,
+
∞
)
,
где последнее условие означает, что при каждом фиксированном
Fo
>
0
функция
Θ(
ρ,
Fo
)
интегрируема с квадратом по пространствен-
ной переменной
ρ
2
[
ν
(
Fo
)
,
+
∞
);
ρ
=
r
r
0
,
Fo
=
at
r
2
0
,
Θ =
T
−
T
0
T
c0
−
T
0
, ζ
=
T
c
−
T
0
T
c0
−
T
0
,
Bi
=
α
λ
r
0
,
(3)
r
— радиальная координата;
t
— время;
T
— температура;
λ
— коэффи-
циент теплопроводности;
a
— коэффициент температуропроводности;
α
— коэффициент теплоотдачи; индекс “c” относится к внешней среде,
индекс “0” — к начальным значениям величин.
Далее предположим, что функции Bi
=
Bi
(
Fo
)
и
ζ
=
ζ
(
Fo
)
, содер-
жащиеся в математической модели (1), (2) и определенные равенства-
ми (3), удовлетворяют стандартным требованиям теоремы существова-
ния и единственности решения рассматриваемой задачи [9]. Переходя
к подвижной системе координат
X
=
ρ/ν
(
Fo
)
, τ
=
Fo
,
(4)
32 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2006. № 1


