
В.В. Кокушкин, М.К. Хомяков, Н.Ю. Овсянникова
6
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. Машиностроение. 2017. № 2
Использование такой модели не дает точного представления о движении
реального ОГБ, масса которого изменяется по мере выгорания топлива, но поз-
воляет оценить диапазон значений кинематических параметров ОГБ на момент
отделения СА.
Модель 2: ОГБ–тело переменной массы (МЦИХ изменяются по известному
линейному закону).
В ходе расчета с использованием данной модели на каждом шаге интегри-
рования проводится пересчет МЦИХ ОГБ. При этом перемещение собственно
центра масс головного блока в инерциальном пространстве не учитывается, что
вносит искажение в картину относительного движения РН и ОГБ. Однако такой
подход позволяет оценить вращательную составляющую движения ОГБ.
Модель 3: ОГБ представлено двумя телами (АТТ и телом переменной мас-
сы), которые соединены связью типа «заделка».
Данная модель лишена недостатков приведенных вариантов представления
ОГБ, к тому же в перспективе может быть использована для реализации сквоз-
ного расчета отделения СА: отделение ОГБ от РН, автономный полет ОГБ и за-
тем отделение СА от ОГБ.
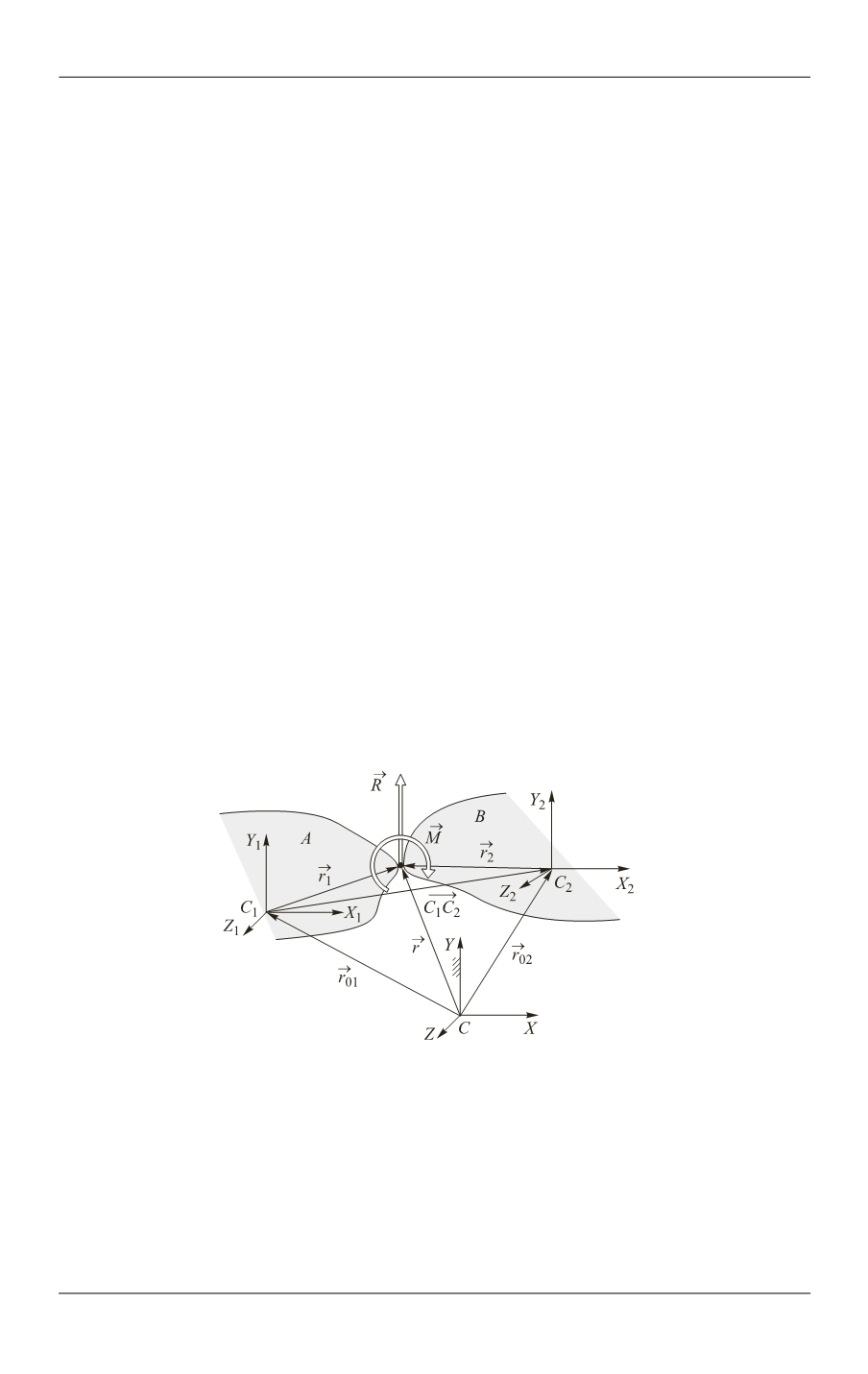
Рассмотрим третий вариант моделирования ОГБ подробнее. Имеем два тела
(рис. 2): тело
А
— АТТ и тело
В
— тело, МЦИХ которого изменяются по извест-
ному закону в зависимости от времени. Поскольку по условию эти тела пред-
ставляют собой один рассматриваемый объект, то объединим тела
А
и
В
связью
типа «заделка» в месте их механического соединения, предотвращая смещение и
поворот тел относительно друг друга. В этой точке прикладываем к телам силы
и моменты реакции связи.
Рис. 2.
Схема для определения реакций в точке связи
Движение тела
А
определяется численным интегрированием уравнений
движения, а кинематические параметры тела
В
переменной массы на каждом
шаге интегрирования — следующими зависимостями [7]:
2
1
;
2 1 1 1 2
,
v v
C C
















