Математическое моделирование динамики температуры солнечных батарей в различных условиях орбитального полета космического аппарата

8 / 18

Математическое моделирование динамики температуры солнечных батарей…
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. Машиностроение. 2016. № 6 11
Поскольку 1, R  cos (1 cos ), H R R R       то уравнения площадей сол-
нечного и земного дисков будут иметь вид:
   
   
2
солн. диска 1 1 С С
2
земн. диска 2 2 З КА
4 sin 2 , arcsin ;
4 sin 2 , arcsin ,
S R L
S R R
    
    
(4)
где С З, R R и КА R — радиусы Солнца, Земли и орбиты КА соответственно; LС —
расстояние от Солнца до КА.
Для нахождения площади видимой части солнечного диска вид.части S необ-
ходимо вычислить площадь теневого участка солнечного диска тен.части, S кото-
рая состоит из площадей сферических треугольников ΔADB и ΔAEB (рис. 6).
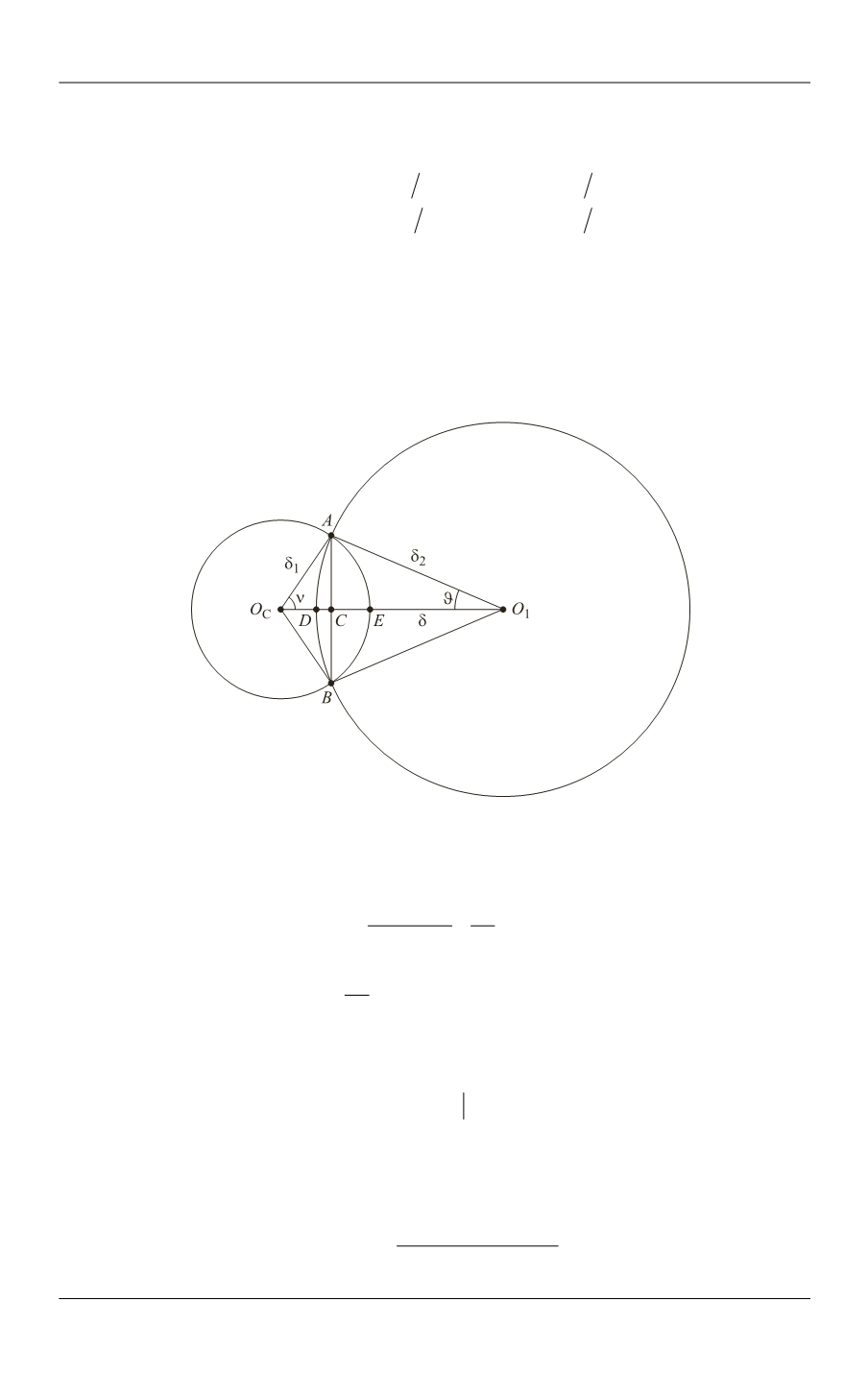
Рис. 6. К расчету площади видимой части солнечного диска
Из сферического треугольника  З АО D и соотношения
земн. диска
З
2 :: ;
AO D
S
S


следует, что 

 емн. диска
З .
2 з AO D S S
Вычисляя сферический избыток [1], определяем площадь сферического
треугольника З : AO D 
     
            
З
2
З З 1 / 2 / 2 .
AO С R S O AC R O AC
Из этого треугольника по теореме косинусов находим угол : 
1 2 2 cos cos cos sin sin cos ;      
1 2
2
cos cos cos
arccos
sin sin
     
   
   
.