
Н.Н. Астахов, Д.Л. Каргу, В.И. Горбулин
8
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. Машиностроение. 2016. № 6
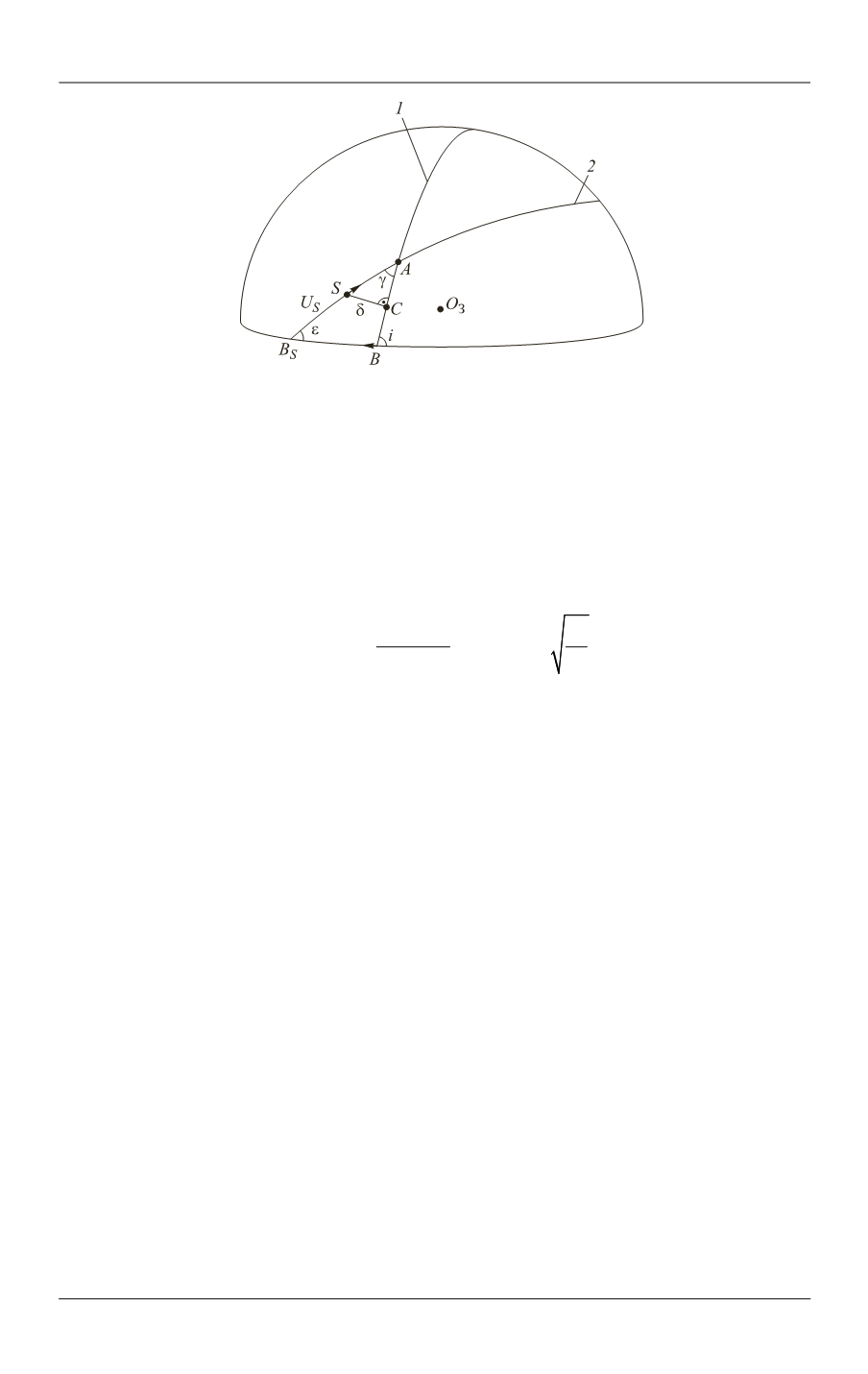
Рис. 3.
Расчет углового расстояния от проекции Солнца (точка
S
) до орбиты КА:
1
— орбита КА;
2
— эклиптика
Динамика рассматриваемого процесса заключается в том, что точка
S
пе-
ремещается по эклиптике, а плоскость орбиты КА непрерывно прецессирует
вдоль экватора. Направления смещения точек
S
и
В
на рис. 3 отмечены стрел-
ками, причем угловая скорость прецессии
прецесс
восходящего узла считается
величиной постоянной и рассчитывается по формулам:
2
прецесс
КА
cos
3
,
i
pT
3
КА
2 ,
a
T
где
2
,
— постоянные гравитационного поля Земли;
а
,
р
,
КА
Т
— большая по-
луось, фокальный параметр орбиты КА и период его обращения по орбите со-
ответственно.
Перемещение точки
S
по эклиптике определяется моделью движения Земли
по орбите вокруг Солнца. Следует отметить, что когда Солнце располагается
достаточно далеко от плоскости орбиты КА, т. е. когда параметр
p
велик, то
тень от Земли не падает на движущийся спутник (этот участок орбиты является
освещенным). В дальнейшем по мере перемещения точки
S
и большого круга
ВСА
по единичной сфере вследствие видимого движения Солнца и прецессии
плоскости орбиты параметр
непрерывно изменяет свое значение. Поскольку
движение точки
S
и прецессии плоскости орбиты не изменяют своего направ-
ления, то неизбежна ситуация, когда точка
S
окажется в плоскости орбиты КА.
Вблизи этого момента будет выполняться условие
пред 1 2
.
(2)
На всем интервале времени
нач.ТУО оконч.ТУО
[
],
t
t
когда выполняется нера-
венство (2), тень от Земли будет периодически падать на движущийся по орбите
КА. Поэтому данный интервал времени
нач. ТУО оконч. ТУО
[
]
t
t
характеризуется
наличием теневых и полутеневых участков орбиты, причем вне этого интервала
таковых участков быть не может. Следовательно, задача состоит в нахождении
















