
Математическое моделирование динамики температуры солнечных батарей…
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. Машиностроение. 2016. № 6
9
таких моментов времени
*
,
t
когда текущее значение расстояния
( )
t
станет
равно заданному
*
пред
( )
.
t
Таким образом, математическая постановка рассматриваемой задачи расчета
границ теневых участков орбиты может быть представлена в следующем виде.
1. Пусть в начальный момент времени
0
t
известны параметры орбиты, в
том числе прямое восхождение восходящего узла
0
0
( )
t
орбиты КА, по-
ложение Солнца на эклиптике
0
0
( ).
S
S
U U t
2.
Требуется
найти
границы
ближайшего
интервала
времени
нач. ТУО оконч. ТУО
[
]
t
t
прохождения КА «Глонасс» теневых участков орбиты,
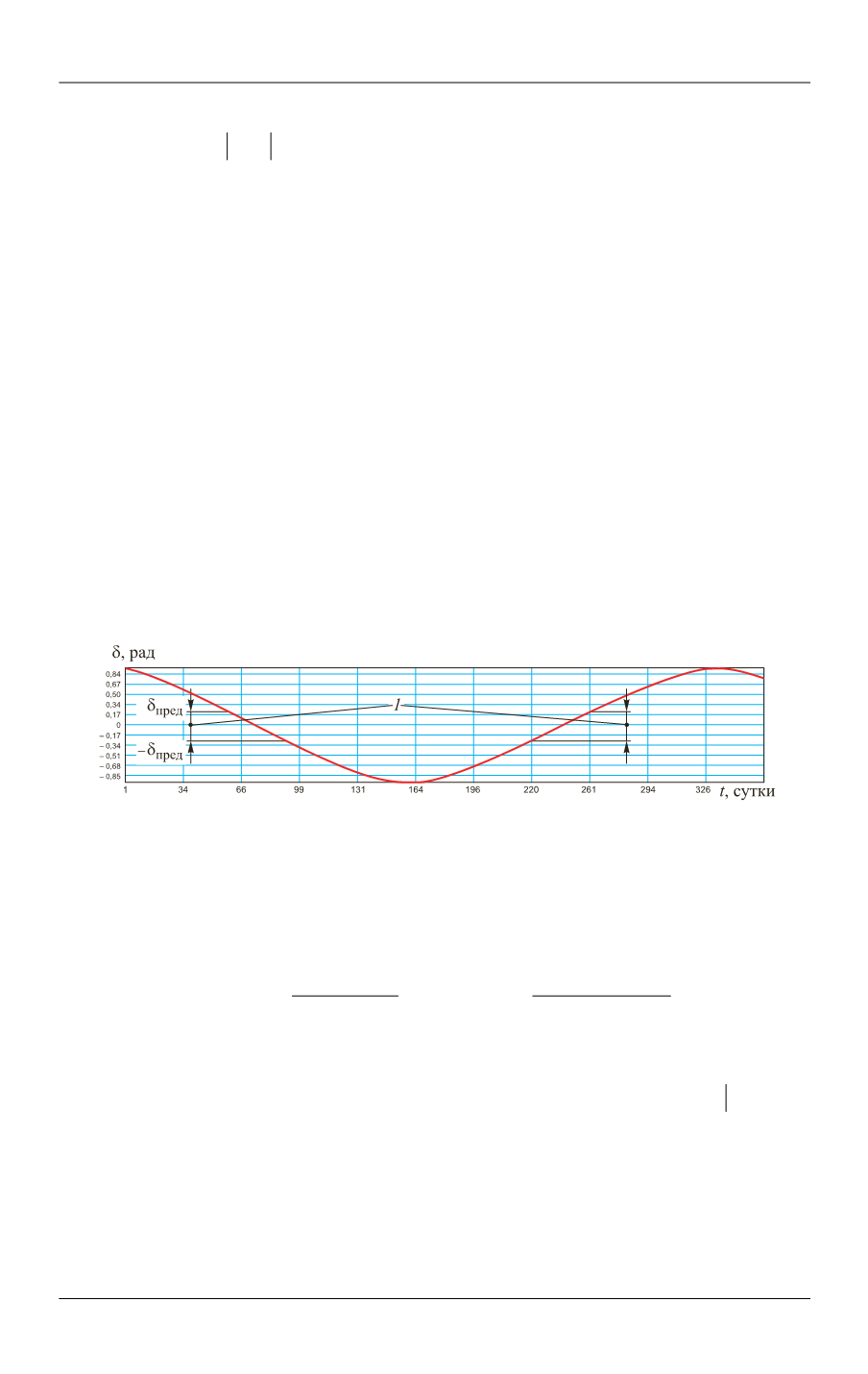
для которых выполняется условие (рис. 4):
нач.ТУО пред
(
)
,
t
оконч.ТУО
пред
(
)
.
t
3. По правилам сферической тригонометрии из треугольника
S
AB B
(см.
рис. 3) находим угол некомпланарности
arccos cos cos sin sin cos
,
i
i
t
где
0
тек 0
.
t
t
t
Рис. 4.
Определение участков орбиты КА (
1
— границы этапа чередования теневых,
полутеневых и освещенных участков орбиты)
Из этого же треугольника по мнемоническому правилу Непера находим дугу
:
S
AB
sin sin
sin
;
sin
S
i
t
AB
cos cos cos
cos
.
sin sin
S
i
AB
Из рис. 4 следует, что дуга
.
S S
AS AB U
Из сферического треугольника
ASC
находим
( ) arcsin sin sin
,
t
AS
следовательно,
*
*
0
,
k
t
t t
f t
0,
где
пред
( ) ( )
f t
t
*
(
t
— корень уравнения
*
0,
f t
определяется чис-
ленным методом, например методом золотого сечения).
Рассмотрев динамику чередования бестеневых и теневых (полутеневых)
участков орбиты, можно более детально проанализировать потоки энергии, по-
ступающие на поверхность КА.
















