
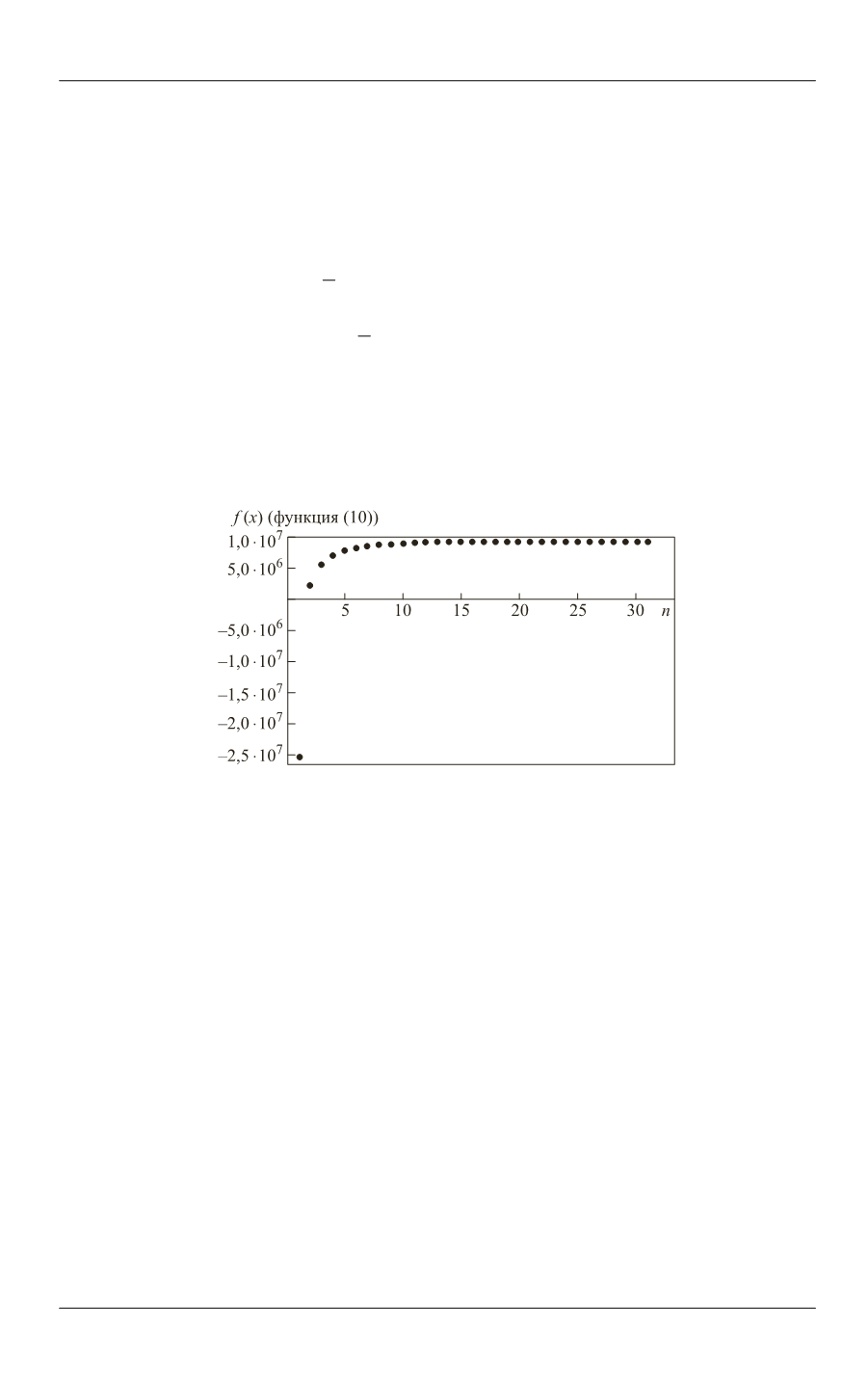
Н.В. Быков, В.В. Зеленцов
138
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. Машиностроение. 2016. № 4
В этом случае с теми же исходными данными при коэффициенте штрафа
0,01
кг
м
2
/
(с
2
∙ Па) для целевой функции приведенного вида результат бу-
дет другой. Дульная скорость составит 1538 м/с при массе снаряда, равной
11,667 кг. Сравним кинетическую энергию боеприпаса в этом и предыдущем
случаях:
2 2 2
2 2 2
1 11,667 кг 1538 м /с
2
1
13,8МДж 5кг 2041 м /с 10,4МДж.
2
В последнем случае эта энергия на 32 % больше, что отвечает реализации
выбранного критерия.
Результат сходимости метода изображен на рис. 4. Видно, что принципи-
альная сходимость метода реализуется приблизительно за 15 поколений.
Рис. 4.
Результат сходимости метода на основе генетического
алгоритма (10)
Следует отметить, что методика позволяет использовать различные форму-
лировки критериев оптимальности и ограничений.
Выводы.
Рассмотрено построение методики проектного синтеза парамет-
ров БУ с гидродинамическим эффектом на основе генетического алгоритма.
Методика позволяет находить оптимальные геометрические и другие парамет-
ры БУ на основе выбранного критерия при наличии заданных ограничений.
Данная методика без ограничений может быть перенесена на любые классы
БУ, в частности артиллерию классических схем, легкогазовые установки и другие.
ЛИТЕРАТУРА
1.
Kureychik V.M., Malyukov S.P., Kureychik V.V., Malyukov A.S
. Genetic Algorithms for
Applied CAD Problems. Springer, 2009. 253 p.
2.
Хоменко Ю.П., Ищенко А.Н., Касимов В.З.
Математическое моделирование внутри-
баллистических процессов в ствольных системах. Новосибирск: Изд-во СО РАН, 1999.
256 с.
3.
Ассовский И.Г
. Физика горения и внутренняя баллистика. М.: Наука, 2005. 357 с.
















