
модели с обоснованиями для расчета движения упругого тела на абсо-
лютно жесткой тележке, скользящей без отрыва на упруговязких ро-
ликах по произвольному двухрельсовому изогнутому и закрученному
пространственному полотну. Настоящая статья является продолжени-
ем исследований плоского движения твердого тела на упругих колесах
(роликах) по криволинейной направляющей [6].
Постановка задачи. Кинематические соотношения.
Рассмотрим
пространственную изогнутую и закрученную полосу с прямолинейны-
ми поперечными сечениями, с двумя направляющими линиями (рель-
сами) и постоянным расстоянием между ними. Геометрия этой полосы
характеризуется параметрами изогнутой в двух плоскостях и нерастя-
жимой средней линии
R
0
(
s
) = [
X
01
(
s
)
X
02
(
s
)
X
03
(
s
)]
T
и углом закру-
чивания
θ
1
(
s
)
поперечного сечения относительно касательной к этой
линии, где
s
— длина дуги, отсчитываемая вдоль этой линии;
X
01
,
X
02
,
X
03
— координаты точки
s
O
средней линии в неподвижной си-
стеме
O
∗
X
1
X
2
X
3
, ось
X
2
которой направлена вверх противоположно
вектору ускорения свободного падения
g
0
(рис. 1).
По полотну на упругих роликах, размеры которых малы, безотрыв-
но движется абсолютно жесткая двухосная тележка с расположенным
на ней деформируемым телом. Связи между полотном и тележкой счи-
таются двухсторонними, безотрывное качение роликов осуществляет-
ся двумя роликами, расположенными в вертикальной плоскости по
разную сторону от рельса, однако в рассматриваемой модели движе-
ния два ролика заменяются одним с единственной точкой контакта.
Трение между полотном и роликами отсутствует, т.е. в рассматри-
ваемой модели полотно считается абсолютно гладкой поверхностью.
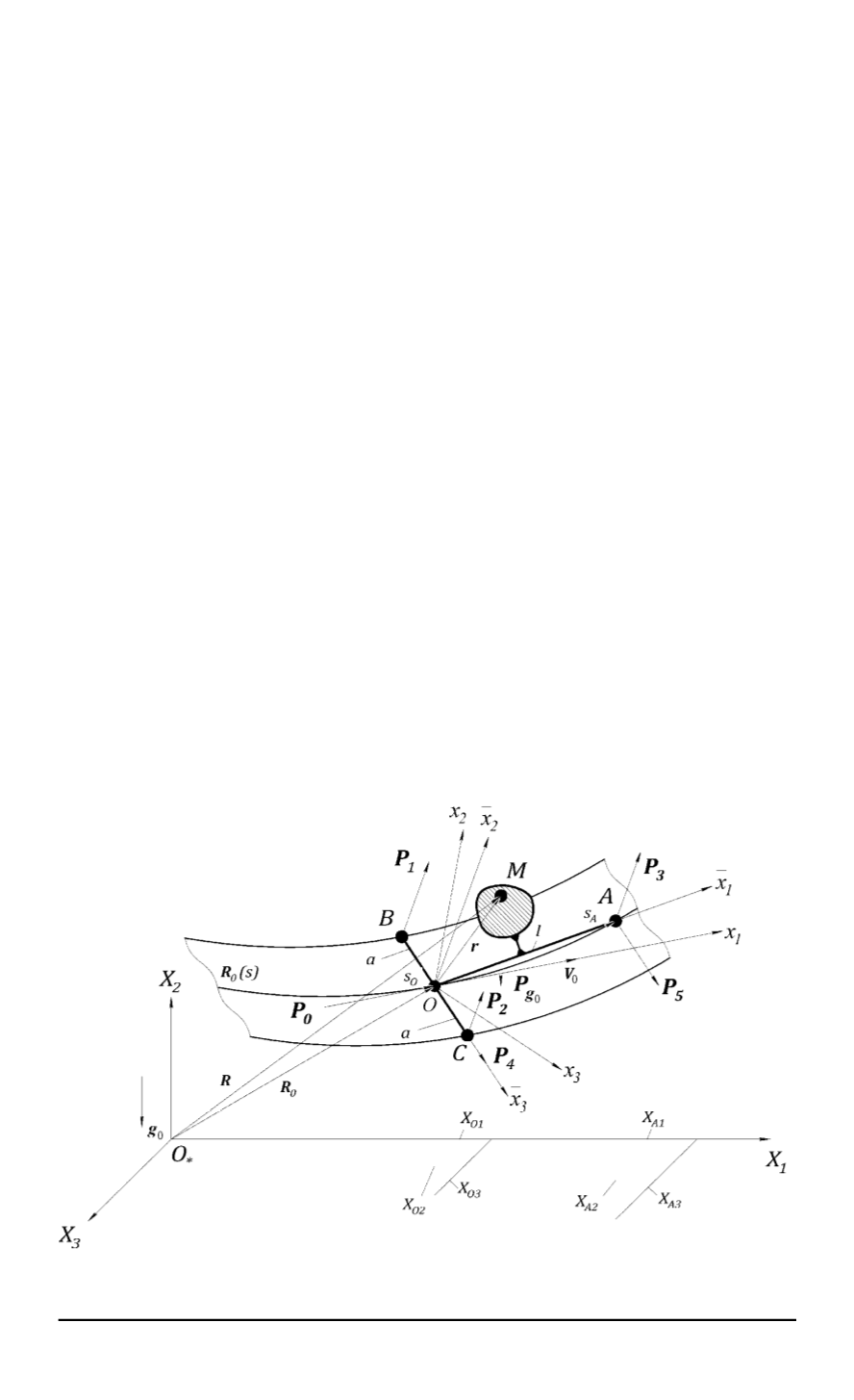
Рис. 1. Геометрическая постановка задачи
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение” 2016. № 2 95
















