
где
ϕ
1
— угловая координата выходного вала идеализированного ре-
дуктора,
ϕ
2
— угловая координата выходного звена привода.
В приведении к частоте выходного вала уравнение (8) с учетом
(9)–(11) можно представить как
J
д
u
2
p
¨
ϕ
1
+
k
p
( ˙
ϕ
1
−
˙
ϕ
2
) +
c
(
ϕ
1
−
ϕ
2
) =
k
м
U
я
−
k
ω
˙
ϕ
1
u
p
R
я
u
p
;
(12)
уравнение моментов на выходном валу в виде
J
н
¨
ϕ
2
−
k
p
( ˙
ϕ
1
−
˙
ϕ
2
)
−
c
(
ϕ
1
−
ϕ
2
) =
−
M
c
;
(13)
уравнение изменения напряжения якоря (при моделировании и в экс-
перименте входной сигнал изменялся по синусоидальному закону) в
виде
U
я
=
U
ян
sin
ωt,
(14)
где
ω
— круговая частота.
Одним из важных этапов моделирования привода является оценка
коэффициентов динамической модели. Именно значения этих коэффи-
циентов отличают привод с ВЗП от приводов с редукторами других
видов. Необходимо определить оценки следующих параметров моде-
ли:
J
д
,
J
н
,
k
p
и
c
. Для этого используют либо результаты эксперимен-
тальных исследований, либо расчеты по теоретическим формулам и
эмпирическим зависимостям. В настоящей работе
J
д
и
J
н
определя-
лись расчетом, а
k
p
и
c
— по экспериментальным кривым.
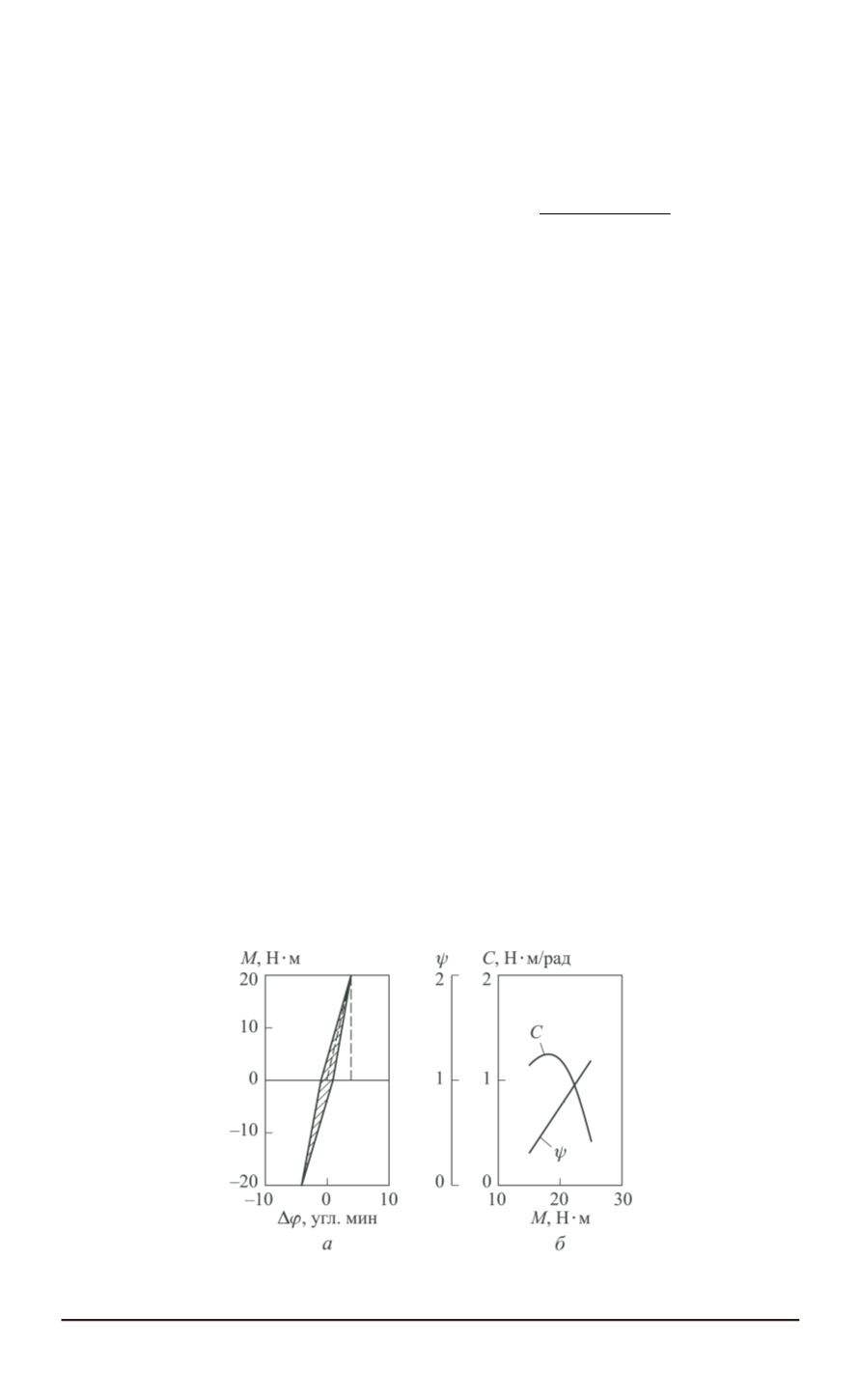
На рис. 3 приведены экспериментальные зависимости
M
=
f
(Δ
ϕ
)
,
c
=
f
(
M
)
и
Ψ =
f
(
M
)
, которые использовались для оценки
k
p
и
c
.
Здесь
M
— момент нагрузки на выходном валу ВЗП,
Δ
ϕ
— угловое
перемещение выходного вала при нагрузке
M
и заторможенном вход-
ном валу редуктора,
с
— крутильная жесткость ВЗП, приведенная к
выходному валу,
Ψ
— коэффициент поглощения. Коэффициентом по-
глощения называют отношение работы диссипативных сил за период
Рис. 3. Оценка жесткости и демпфирования ВЗП
122 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2015. № 5

















