
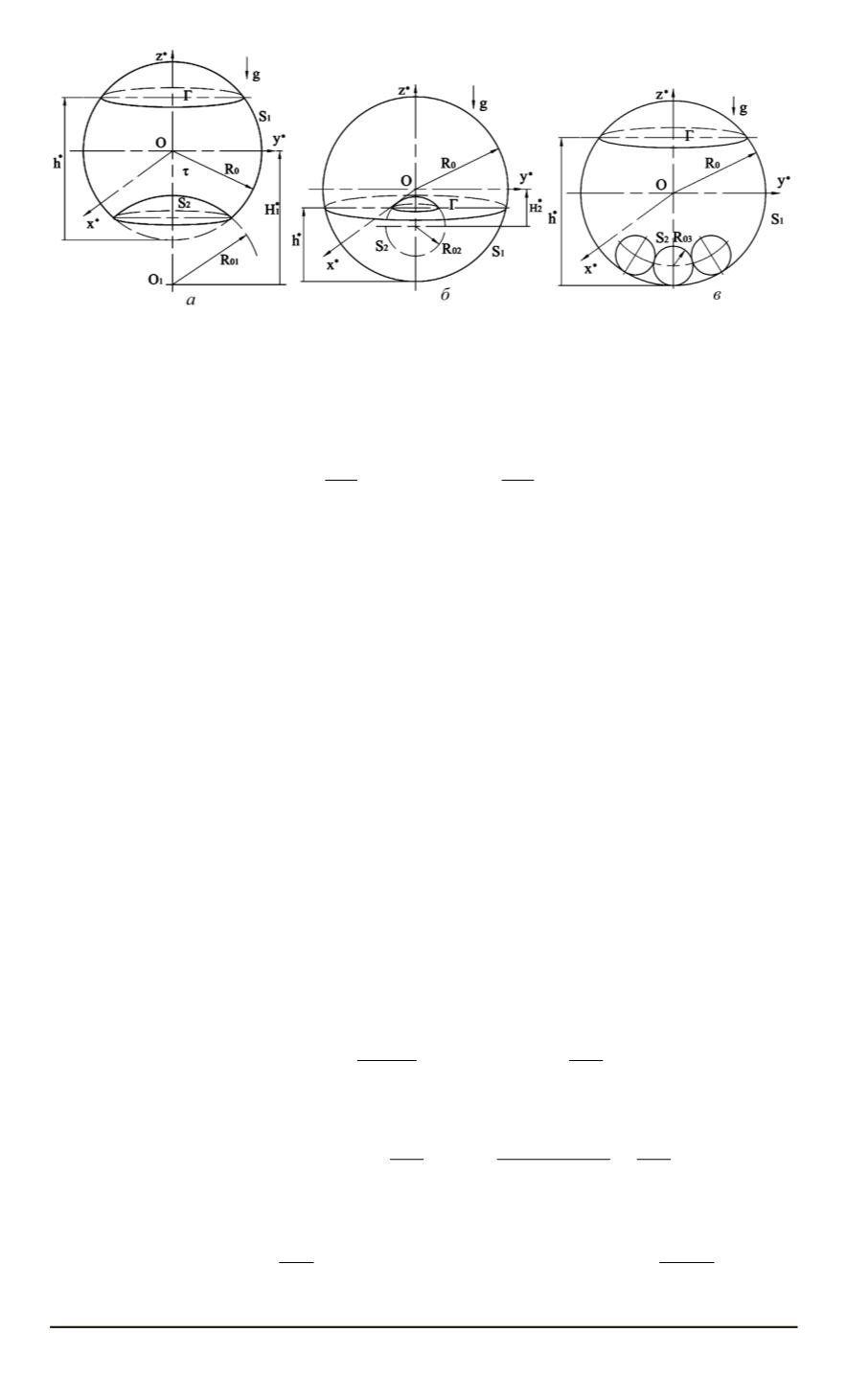
Основные обозначения и системы координаты
задача для определения потенциала скоростей
Φ(
R, θ, η
)
во всех слу-
чаях имеет вид [1–8]
ΔΦ = 0
в
τ,
∂
Φ
∂n
= 0
на
S,
∂
Φ
∂z
=
λ
Φ
на
Γ
0
,
(1)
где
τ
— область, заполненная жидкостью;
S
— смачиваемые поверх-
ности;
Γ
0
— свободная поверхность;
n
— вектор внешней нормали
к поверхности
S
;
λ
=
ω
2
R
0
/g
— собственное значение задачи,
g
—
ускорение свободного падения.
Краевая задача (1) имеет эквивалентную вариационную формули-
ровку: найти минимум функционала
F
(Φ) =
Z
τ
(
∇
Φ)
2
dτ
−
λ
Z
Γ
0
Φ
2
d
Γ
.
(2)
Будем искать решение вариационной задачи (2) в виде
Φ(
R, θ, η
) =
U
(
R, θ
)
H
m
(
η
)
, H
m
(
η
) =
sin (
mη
)
,
cos (
mη
)
,
m
= 0
,
1
,
2
, . . . .
(3)
Решение первой (см. рисунок,
а
) и второй (см. рисунок,
б
) задач
методом Трефтца
. Подставляя выражение (3) в (2), функционал для
каждой задачи можно выписать следующим образом:
F
(
U
) = (
h
−
1)
2
θ
0
Z
θ
1Γ
U
Γ
A
Γ
U
sin
θ
cos
2
θ
dθ
+
θ
H
1
Z
θ
0
U
S
1
∂U
∂R
S
1
sin
θdθ
+
+
R
1
π
Z
θ
H
1
U
S
2
cos(
θ
+
θ
2
)
∂U
∂R
S
2
−
sin(
θ
+
θ
2
)
r
2
∂U
∂θ
S
2
!
×
×
cos
θ
dr
2
dθ
−
r
2
sin
θ dθ
−
λ
(
h
−
1)
2
θ
0
Z
θ
1Γ
U
2
Γ
sin
θ
cos
3
θ
dθ,
(4)
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение” 2015. № 2 85

















