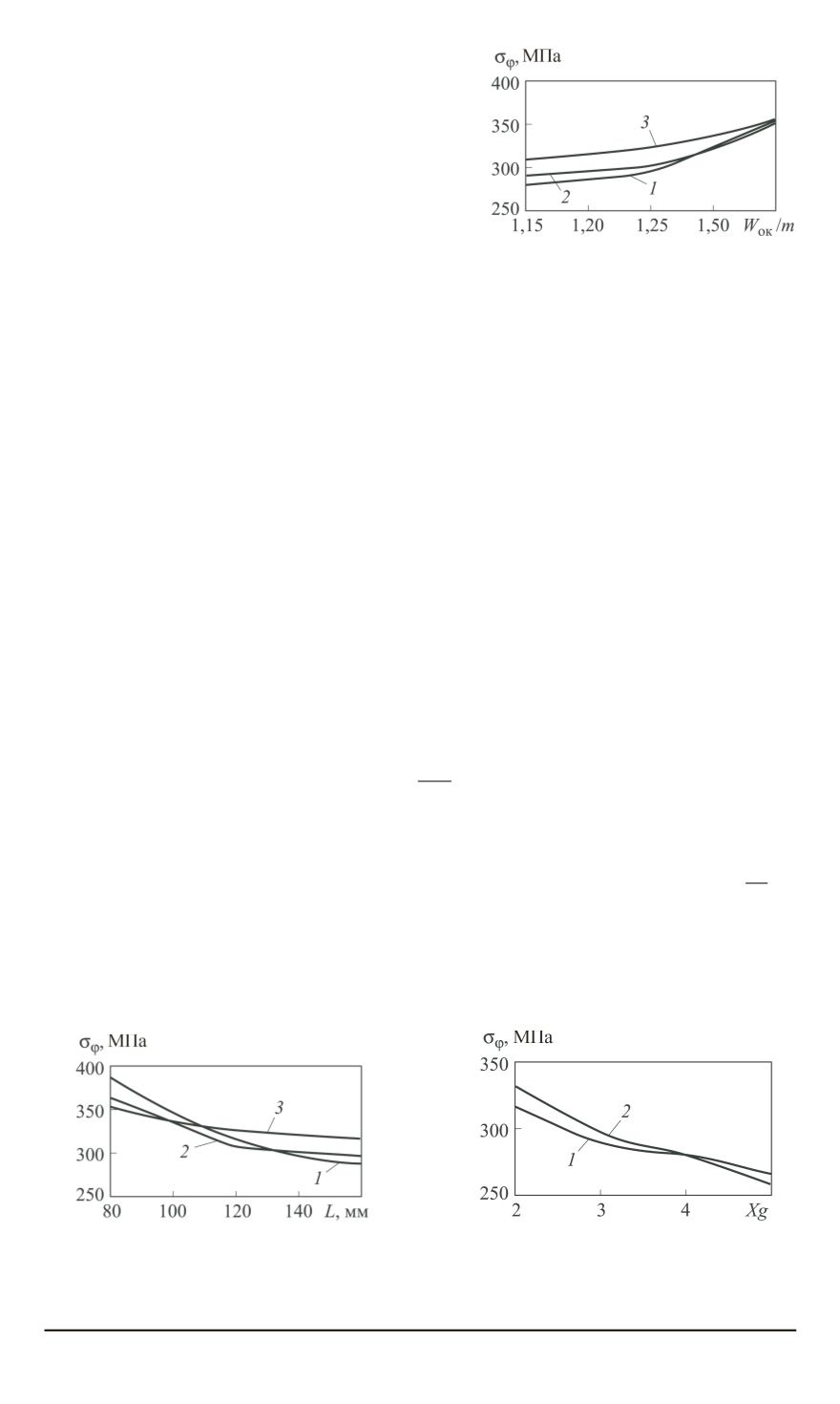
Рис. 8. Влияние
W
0к на напря-
жения (вторая форма кулачка,
β
= 35
◦
):
1
—
h
1
= 1
,
25
;
2
—
h
1
= 1
,
5
;
3
—
h
1
= 1
,
75
рассматриваемой передачи значение
W
0
к
= 1
,
15
m
является оптимальным.
При меньших значениях
W
0
к
на но-
минальном режиме работы происходит
интерференция зубьев.
Рассмотрим влияние длины гибкого
колеса на напряжения в случае, когда
оно выполнено в виде стакана с гиб-
ким дном и фланцем для присоедине-
ния к валу. Наружный диаметр фланца
d
1
= 100
мм. Очевидно, что уменьше-
ние длины оболочки гибкого колеса
L
приводит к увеличению напряжений в
зубчатом венце (рис. 9). При
h
1
= 1
,
25
мм уменьшение
L
от 160 мм
до 120 мм незначительно увеличивает напряжения, а уменьшение
L
от 120 мм до 80 мм увеличивает максимальные окружные напряже-
ния
σ
ϕ
на 25%. При
h
1
= 1
,
5
мм зависимость
σ
ϕ
(
L
)
имеет аналогич-
ный характер. При
h
1
= 1
,
75
мм рассматриваемая зависимость
σ
ϕ
(
L
)
является практически линейной, а уменьшение
L
от 160 мм до 80 мм
приводит к увеличению напряжений на 11%. Из приведенных зависи-
мостей следует, что оптимальная толщина зубчатого венца
h
1
зависит
от длины гибкого колеса
L
.
При получении зависимости напряжений от коэффициента смеще-
ния гибкого колеса
X
g
коэффициент смещения жесткого колеса вы-
числялся по формуле
X
B
=
X
g
+
W
0
m
−
1
. Здесь
W
0
— максимальная
радиальная деформация зубчатого венца гибкого колеса. Необходи-
мо отметить, что наружный диаметр гибкого подшипника не прини-
мался по ГОСТ 23179–78, а вычислялся по формуле
D
= 2
m
z
g
2
+
+
x
g
−
h
a
−
c
−
2
h
1
. Если
D
принимать по ГОСТ, то при изменении
коэффициента смещения
X
g
необходимо изменять толщину зубчатого
венца
h
1
. В этом случае невозможно отличить влияние на напряжения
Рис. 9. Влияние
L
на напряжения
σ
ϕ
:
1
—
h
1
= 1
,
25
мм;
2
—
h
1
= 1
,
5
мм;
3
—
h
1
= 1
,
75
мм
Рис. 10. Влияние
X
g
на напряже-
ния
σ
ϕ
:
1
—
h
1
= 1
,
25
мм;
2
—
h
1
= 1
,
5
мм
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение” 2014. № 6 27


