где
y
1(2)
=
h
0
cos
ϑ
−
l
E
sin
ϑ
+
l
0
(
α
0
−
ϑ
1(2)
);
(4)
ϑ
2
= arcsin(cos(
π
−
γ
2
) sin
ϑ
)
(5)
— угол наклона КА для второй опоры).
Для
δy
1(2)
= 0
определим текущие значения для
y
и
ϑ
, полученных
при интегрировании уравнений (1):
α
1(2)
= arcsin
y
+
l
E
sin
ϑ
−
h
0
cos
ϑ
l
0
+
ϑ
1(2)
;
H
1(2)
=
l
0
sin
α
1(2)
+
l
E
;
L
1(2)
=
l
0
cos
α
1(2)
+
l
E
;
l
ам
1(2)
=
q
(
H
+
h
1(2)
)
2
+ (
L
1(2)
−
l
E
)
2
;
δ
1(2)
=
l
ам
1(2)
−
l
ам
1(2)
— изменение длины амортизатора;
x
1
=
l
0
cos(
α
1
−
ϑ
) +
l
E
cos
ϑ
+
h
0
sin
ϑ
;
x
2
= cos
γ
2
(
l
0
cos(
α
2
−
ϑ
2
) +
l
E
cos
ϑ
2
+
h
0
sin
ϑ
2
);
β
1(2)
= arcsin
L
1
−
l
E
l
ам
1(2)
.
(6)
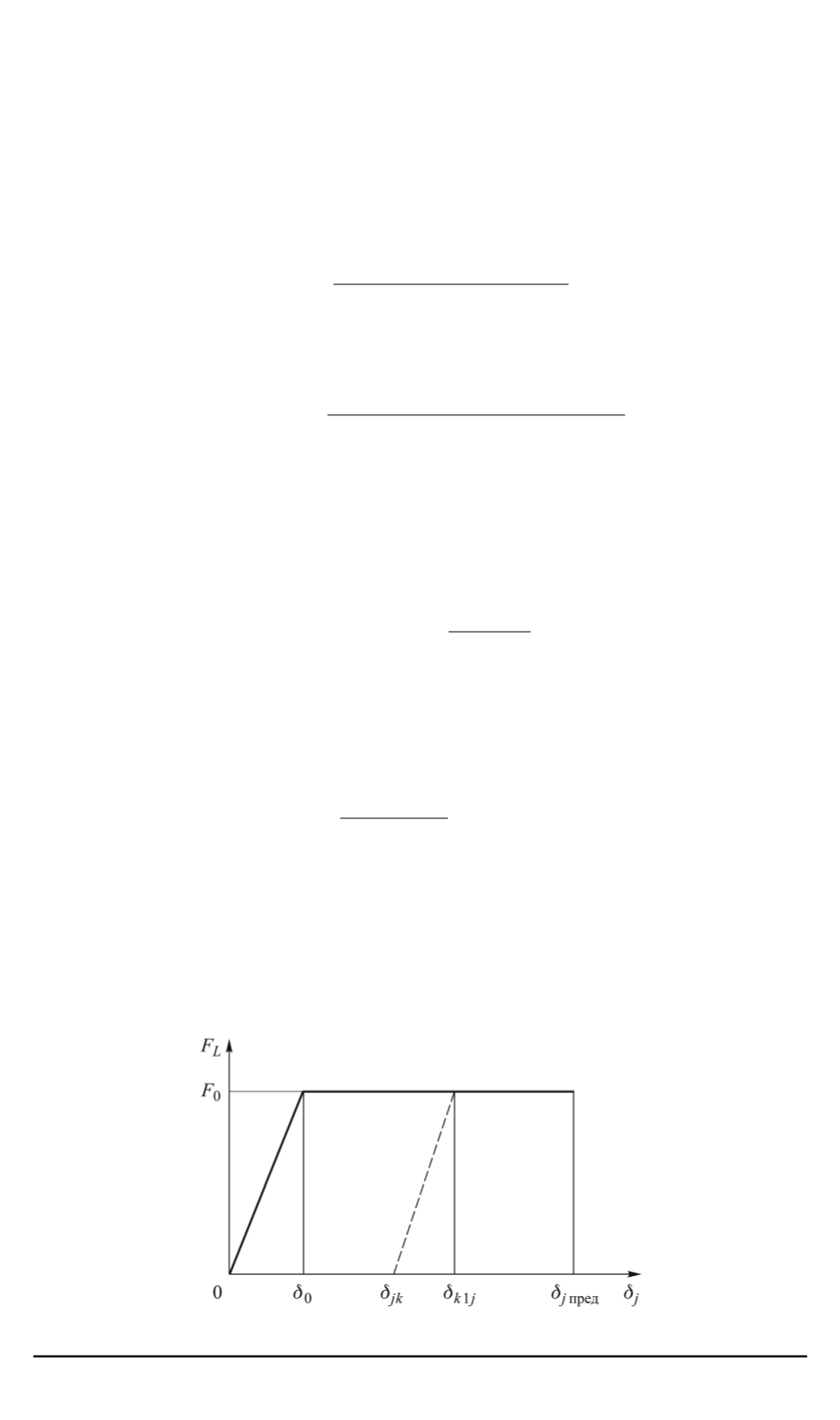
В соответствии с рис. 4 по
δ
1
определяем значение силы в аморти-
заторе:
F
L
1(2)
(
δ
) =
0
, δ
1(2)
≤
δ
jk
;
F
0
δ
1(2)
−
δ
k
1
δ
0
, δ
jk
< δ
1(2)
< δ
k
1(2)
;
F
0
, δ
1(2)
≥
δ
k
1(2)
,
(7)
где
δ
0
— начальное значение упругой зоны деформации амортизатора;
δ
k
1
j
— значение упругой зоны деформации амортизатора;
δ
jk
— началь-
ное значение деформации при
j
-м касании опоры поверхности,
F
0
—
сила при разрушении амортизатора.
Рис. 4. График изменения силы в амортизаторе
30 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2014. № 1


