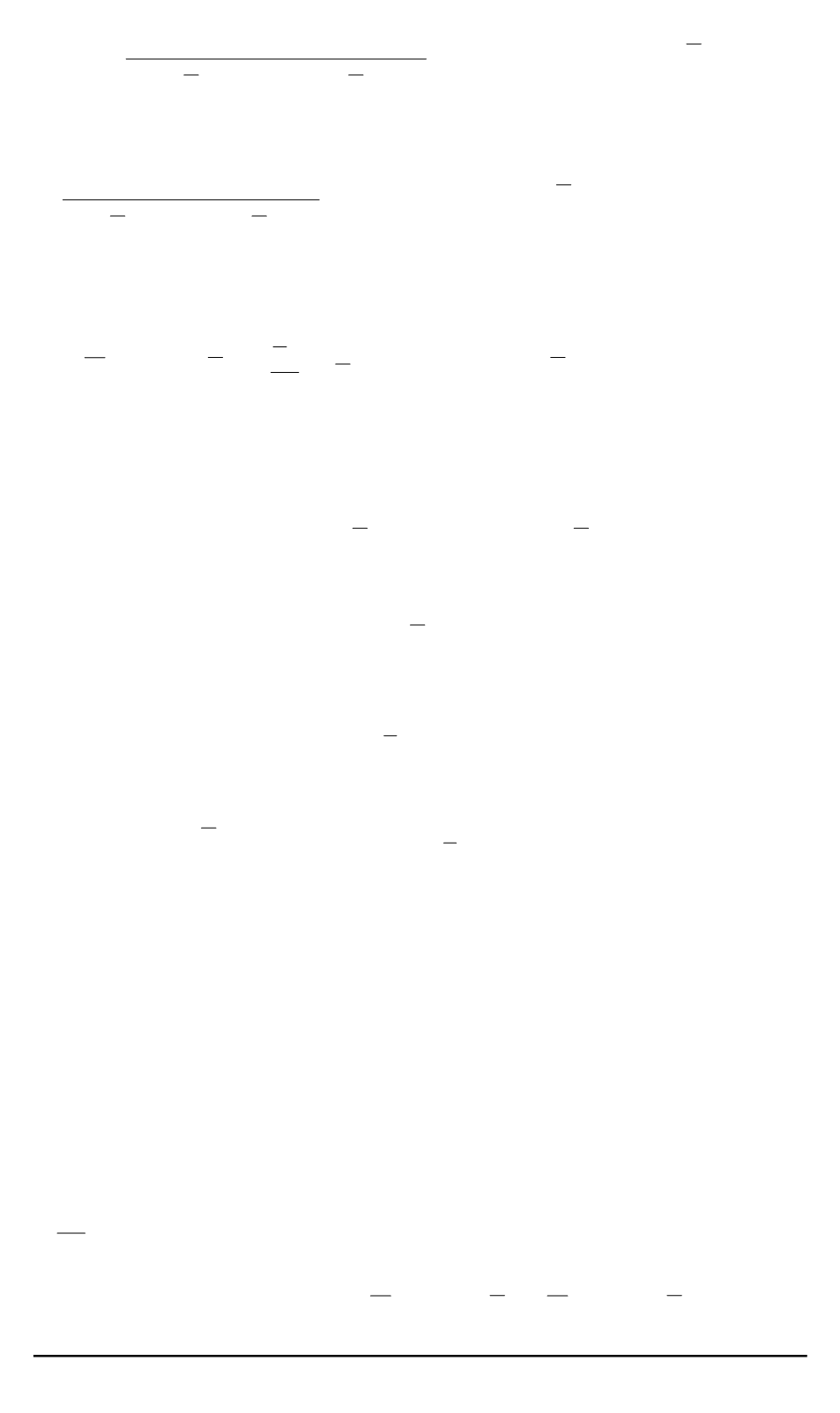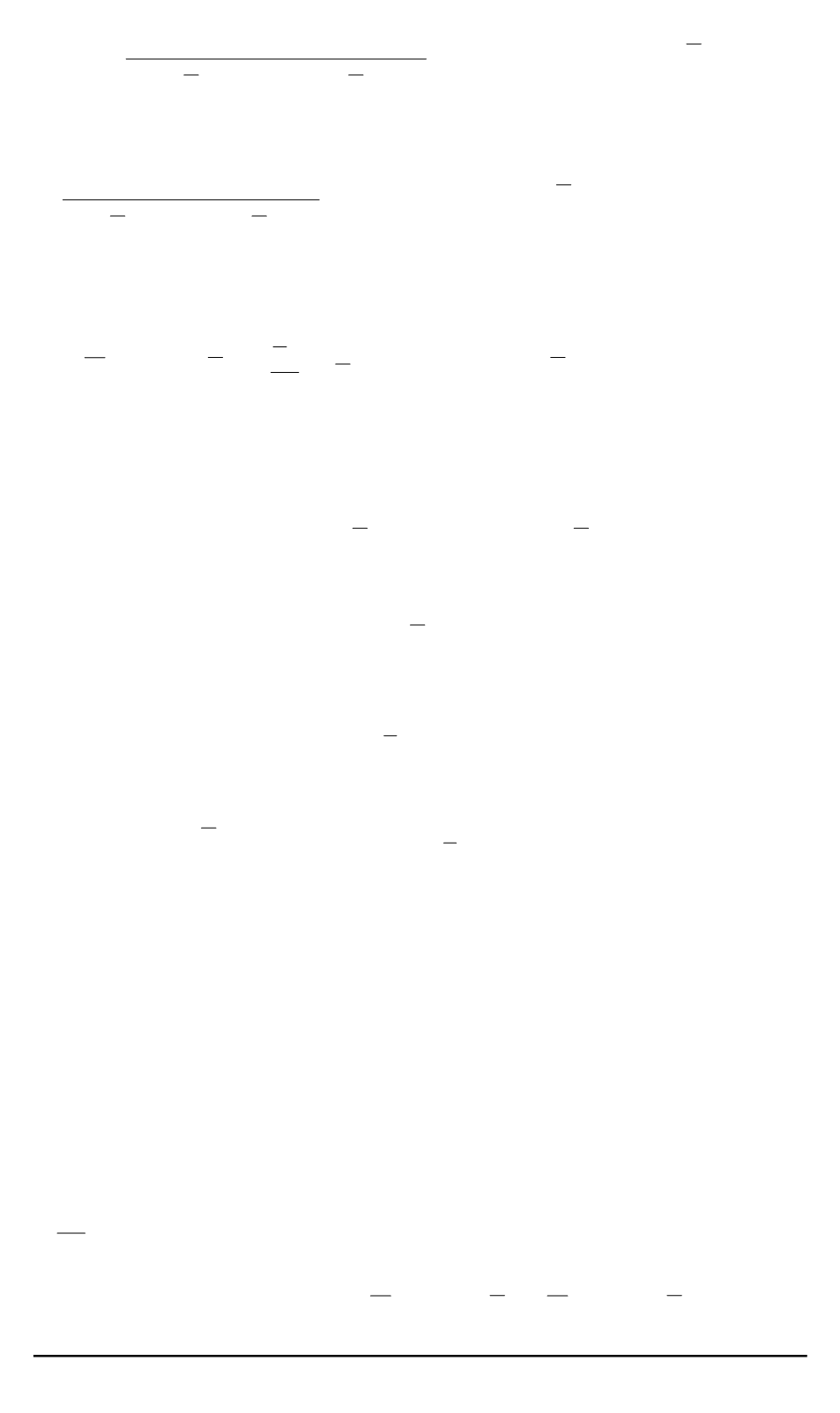
+
[
i
+ 1 + (
k
+ 0
,
5)]
λ
n
cos 2
α
2
h
h
00
ci
+1
,k
α, θ, θ
0
, h
i
2
1 + cos
δ
00
ci
+1
,k
α, θ, θ
0
, h
−
−
[
i
+ (
k
+ 0
,
5)]
λ
n
cos 2
α
2
h
h
00
ci,k
α, θ, θ
0
, h
i
2
1 + cos
δ
00
ci,k
α, θ, θ
0
, h
cos
χ
(
θ
) sin
θdθ
(6)
или
V
(
n
)
ci,k
α, θ
0
, h
=
a
i
2
π
π
Z
0
γ
i
(
α, θ
)
ω
ik
α, θ, θ
0
, h
cos
χ
(
θ
) sin
θdθ,
где через
ω
ik
обозначено выражение в фигурных скобках формулы (6).
Суммируя по всем панелям отображенного крыла, получим
ˉ
V
(
n
)
ck
α, θ
0
, h
=
n
−
1
X
i
=0
ˉ
V
(
n
)
ci,k
α, θ
0
, h .
Распределение вихревой плотности по хордам панелей отображен-
ного
ˉ
γ
i
(
α, θ
)
и реального
ˉ
γ
i
α, θ, h
крыльев представляется прибли-
женно тригонометрическими рядами [2]:
ˉ
γ
i
(
α, θ
) = 2
"
A
0
i
(
α
) ctg
θ
2
+
p
X
q
=1
A
qi
(
α
) sin
qθ
#
,
ˉ
γ
i
α, θ, h
= 2
"
B
0
i
α,
ˉ
h
ctg
θ
2
+
p
X
q
=1
B
qi
α,
ˉ
h
sin
qθ
#
.
Распределение вихревой плотности модели отображенного крыла
считается заданным — полученным из расчета крыла в свободном
потоке (по методике [2]), соответственно, заданными принимаются и
коэффициенты ряда
A
0
i
(
α
)
, A
1
i
(
α
)
, . . . , A
pi
(
α
)
.
Уравнение непроницаемости. Вычисление величины и закона
распределения вихревой плотности модели реального крыла око-
ло экрана.
С учетом действия вихрей модели отображенного крыла
уравнение непроницаемости реального крыла в точке среднего сече-
ния
k
-й панели будет иметь вид
1
2
π
π
Z
0
"
n
−
1
X
i
=0
ˉ
γ
i
α, θ,
ˉ
h K
i,k
(
α, θ, θ
0
) sin
θdθ
+
+
V
(
n
)
п
k
α, θ
0
, h
+
V
(
n
)
с
k
α, θ
0
, h
= sin
α,
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2006. № 2 11