Таблица 2
Коэффициенты
Угол
α/
2
C
i
k
i
, x
i
sin 1
◦
30
0
=
= 0
,
02618
sin 2
◦
51
0
=
= 0
,
04972
sin 5
◦
42
0
=
= 0
,
09932
sin 8
◦
17
0
=
= 0
,
14407
k
1
1,342615
1,706720
2,473811
3,165739
C
1
x
1
– 0,15543
– 0,257321
– 0,472589
– 0,666766
C
2
k
2
1,29995
1,554245
2,089991
2,573244
x
2
– 0,144385
– 0,212243
– 0,355206
– 0,484161
C
3
k
3
1,035493
1,222708
1,617127
2,048302
x
3
– 0,019714
– 0,281770
– 0,478796
– 0,546557
Приведенные аппроксимационные зависимости
k, x
=
f
α
2
по-
лучены с помощью той же прикладной программы APROKSIM-1 по
двум точкам при условии прямолинейной графической зависимости
вида
y
=
a
+
bx
между переменными параметрами (рис. 3,
а
и
б
). Ис-
пользуя аппроксимационные зависимости второго уровня (4), (5), (6),
представляется возможным провести не табличное, а расчетное опре-
деление искомых коэффициентов
C
1
,
С
2
и
C
3
, учитывая произвольные
значения переменных параметров
λ
и угла
α
2
.
Для автоматизированного расчета этих коэффициентов по указан-
ным уравнениям была разработана прикладная программа
RAS CIC. PAS [2].
Угол поворота
ϕ
в торцевом стыке (рис. 4) можно определить по
известным зависимостям:
ϕ
=
k
(1
−
χ
)
M
I
,
мкм/мм
,
(7)
где
k
— коэффициент контактной податливости,
k
=
Cmσ
m
−
1
0
,
мкм/Н
∙
мм
−
2
;
C
— коэффициент, зависящий от геометрии поверхности
и физических свойств материалов сопрягаемых деталей. Для стальных
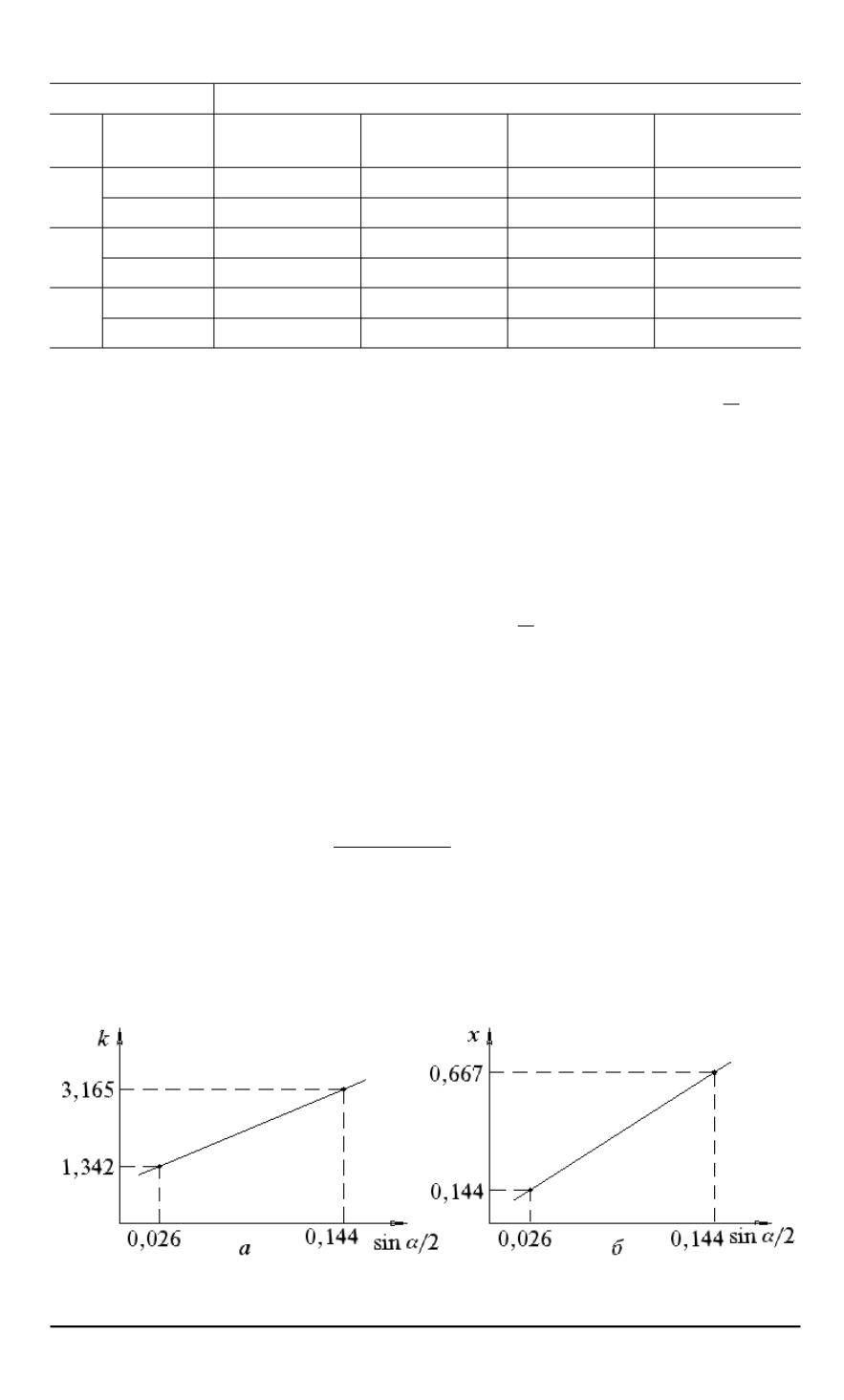
Рис. 3. Графики аппроксимационных зависимостей:
а
–
k
=
f
(
α/
2)
;
б
—
x
=
f
(
α/
2)
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2006. № 1 77


