Компонент
Δ
P
τ
представляет собой функцию, зависящую от пре-
дела текучести суспензии и геометрических параметров зазора:
Δ
P
τ
=
f
(
τ
y
, L, h
)
.
(9)
В общем виде зависимость (9) для дросселя с кольцевым рабочим
зазором, в котором действуют сдвиговые напряжения, можно записать
как
Δ
P
τ
=
cτ
y
(
H
)
L
h
,
(10)
где
c
— коэффициент, зависящий от отношения
Δ
P
τ
/
Δ
P
η
(согласно
данным работы [9]
c
= 2
для
Δ
P
τ
/
Δ
P
η
1
и
c
=3
для
Δ
P
τ
/
Δ
P
η
>
100
).
Для инженерных расчетов при определении предела текучести
можно использовать метод, когда экспериментально измеренной зави-
симости сдвиговых напряжений в МР жидкости от магнитной индук-
ции приложенного поля ставится в соответствие полином, например
τ
y
=
k
1
B
f
+
k
2
B
2
f
,
(11)
где
k
1
, k
2
— постоянные коэффициенты, определяемые графически;
B
f
— индукция магнитного поля в МР жидкости.
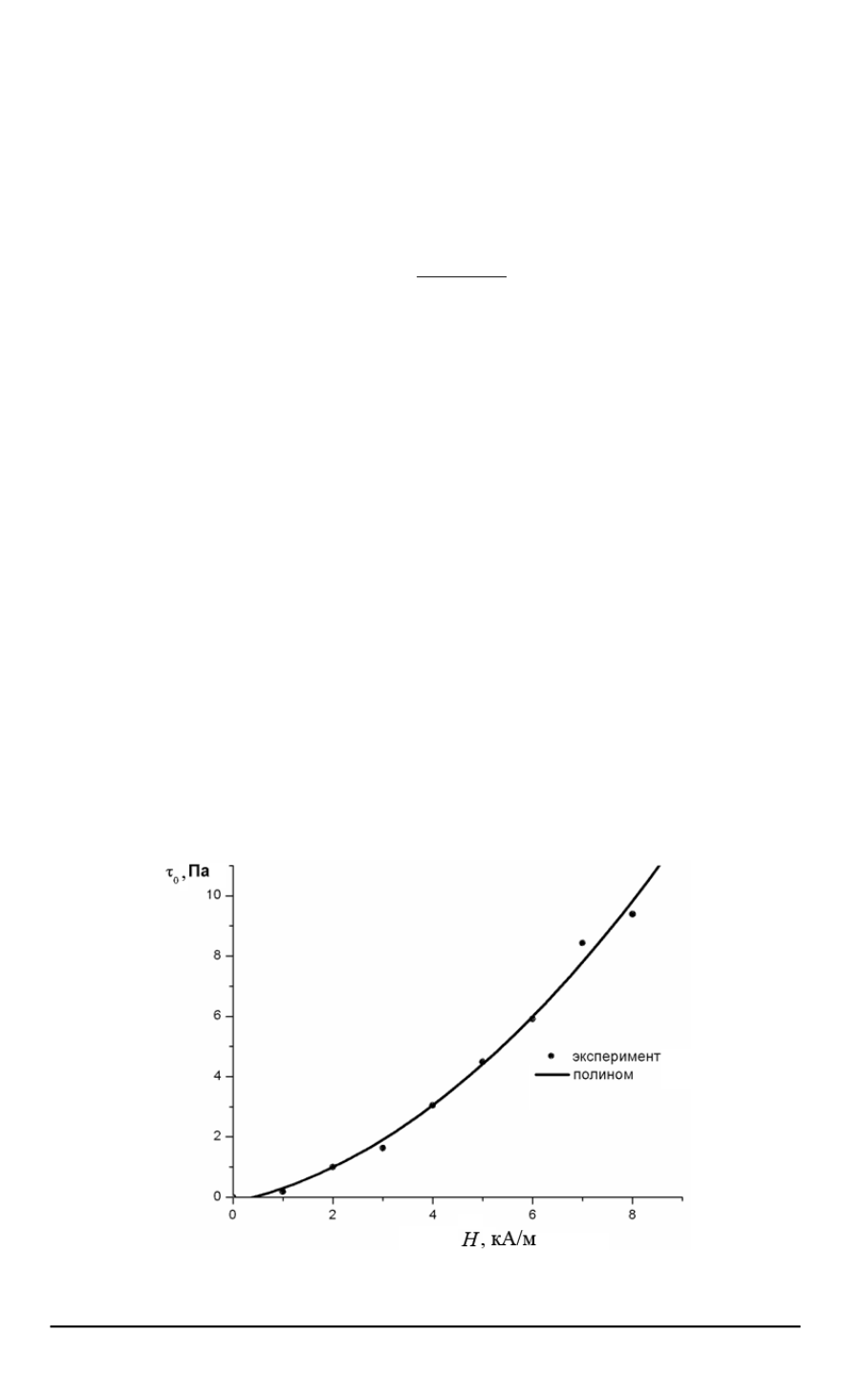
Результаты экспериментов, проведенных с использованием реоме-
тра (см. рис. 3), по определению предела текучести МР жидкости в
зависимости от приложенного магнитного поля приведены на рис. 5.
Для полученной зависимости была предложена модель на основе
полинома вида
τ
0
=
А
0
H
+
A
1
H
2
,
(12)
где
А
0
= 0
,
36021
;
А
1
= 0
,
11124
рассчитаны аналитически.
Магнитная модель МР дросселя.
Дифференциальное уравнение
токов и напряжений, действующих в электромагнитной катушке, мож-
Рис. 5. График зависимости предела текучести МР жидкости от напряженности
внешнего магнитного поля
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2007. № 4 65


