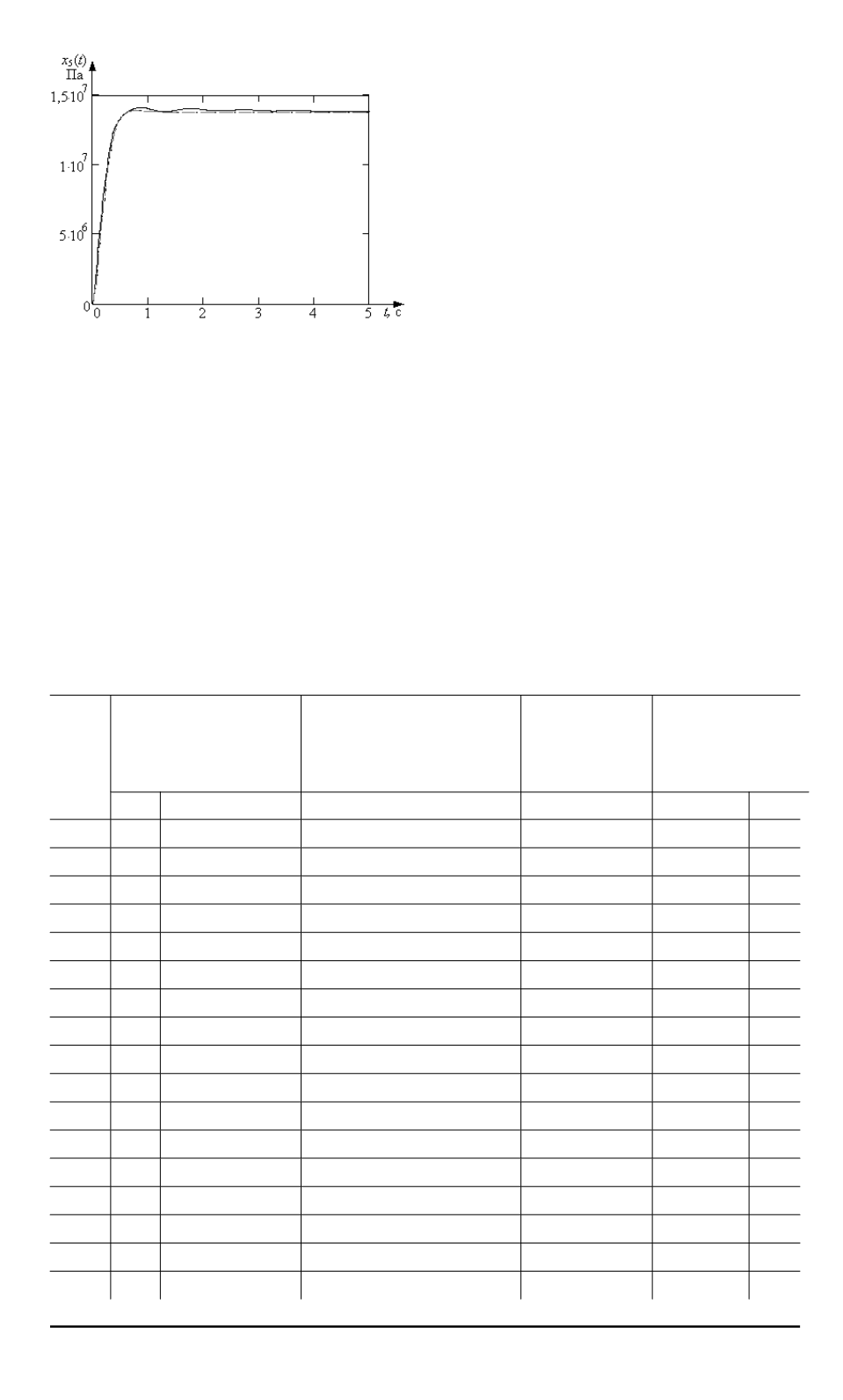
Рис. 6. Результаты расчета сигнала
x
5
(
t
)
при оптимальном значении
K
рег
по проекционно-матричному методу
(– – –) в сравнении с решением, по-
лученным по методу Рунге-Кутта,
(——) при заданном эталонном сигна-
ле (— - — - —)
котором в данной системе дости-
гается решение поставленной зада-
чи стабилизации давления в паро-
генераторе. Как следует из графи-
ка (рис. 6), найденное для системы
(при оптимальной величине
K
рег
)
значение сигнала
x
5
(
t
)
— давле-
ние перед регулирующей задвиж-
кой — достаточно точно совпадает
с заданным (эталонным) переход-
ным процессом для этого сигнала.
В качестве эталонного был принят
этот сигнал, потому что именно пе-
ред регулирующей задвижкой наб-
людались максимальные, а значит,
и наиболее опасные, по амплитуде
колебания давления. Результаты сравнения точного и приближенного
решений приведены в табл. 2.
Таблица 2
Сравнение точного и приближенного решений задачи синтеза
№п/п
Точное решение ме-
тодом Рунге-Кутта
Приближенное
решение проекционно-
матричным методом в
базисе из БИФ
Заданное
значение
(эталон)
Погрешность
t
i
x
5
i
x
l
5
i
x
э
5
i
Δ
, абс
δ
, %
0 0
0
1,43
∙
10
5
1,430
∙
10
5
1,430
∙
10
5
100,0
1 0,25 9,719
∙
10
6
8,82
∙
10
6
8,820
∙
10
6
8,990
∙
10
5
10,2
2 0,5 1,325
∙
10
7
1,32
∙
10
7
1,319
∙
10
7
6,000
∙
10
4
0,5
3 0,75 1,400
∙
10
7
1,39
∙
10
7
1,389
∙
10
7
1,100
∙
10
5
0,8
4 1 1,402
∙
10
7
1,384
∙
10
7
1,384
∙
10
7
1,800
∙
10
5
1,3
5 1,25 1,382
∙
10
7
1,380
∙
10
7
1,380
∙
10
7
2,000
∙
10
4
0,1
6 1,5 1,391
∙
10
7
1,380
∙
10
7
1,380
∙
10
7
1,100
∙
10
5
0,8
7 1,75 1,401
∙
10
7
1,380
∙
10
7
1,380
∙
10
7
2,100
∙
10
5
1,5
8 2 1,395
∙
10
7
1,380
∙
10
7
1,380
∙
10
7
1,500
∙
10
5
1,1
9 2,25 1,387
∙
10
7
1,380
∙
10
7
1,380
∙
10
7
7,000
∙
10
4
0,5
10 2,5 1,390
∙
10
7
1,380
∙
10
7
1,380
∙
10
7
1,000
∙
10
5
0,7
11 2,75 1,394
∙
10
7
1,380
∙
10
7
1,380
∙
10
7
1,400
∙
10
5
1,0
12 3 1,390
∙
10
7
1,380
∙
10
7
1,380
∙
10
7
1,000
∙
10
5
0,7
13 3,25 1,386
∙
10
7
1,380
∙
10
7
1,380
∙
10
7
6,000
∙
10
4
0,4
14 3,5 1,388
∙
10
7
1,380
∙
10
7
1,380
∙
10
7
8,000
∙
10
4
0,6
15 3,75 1,388
∙
10
7
1,380
∙
10
7
1,380
∙
10
7
8,000
∙
10
4
0,6
16 4 1,386
∙
10
7
1,380
∙
10
7
1,380
∙
10
7
6,000
∙
10
4
0,4
108 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2007. № 2


