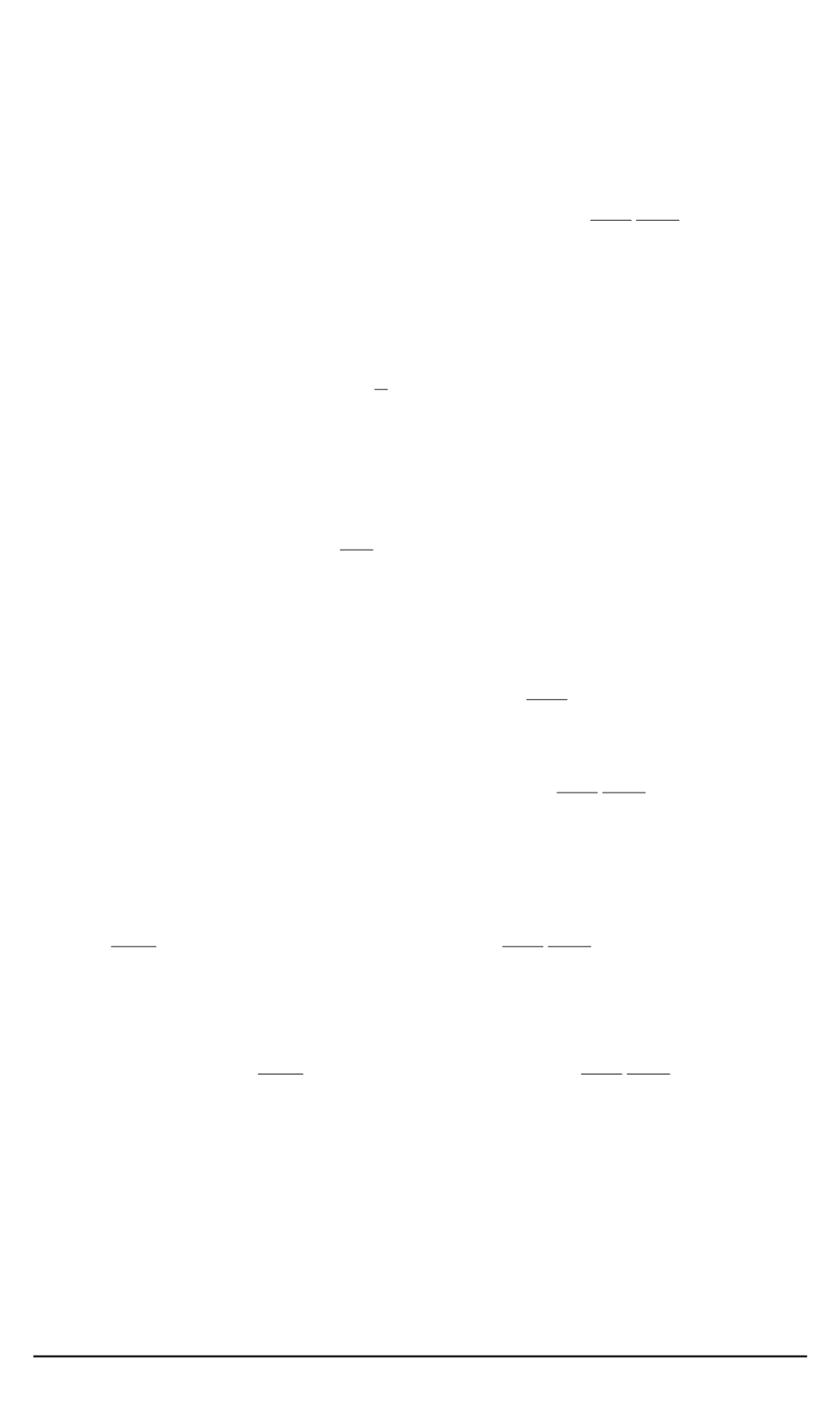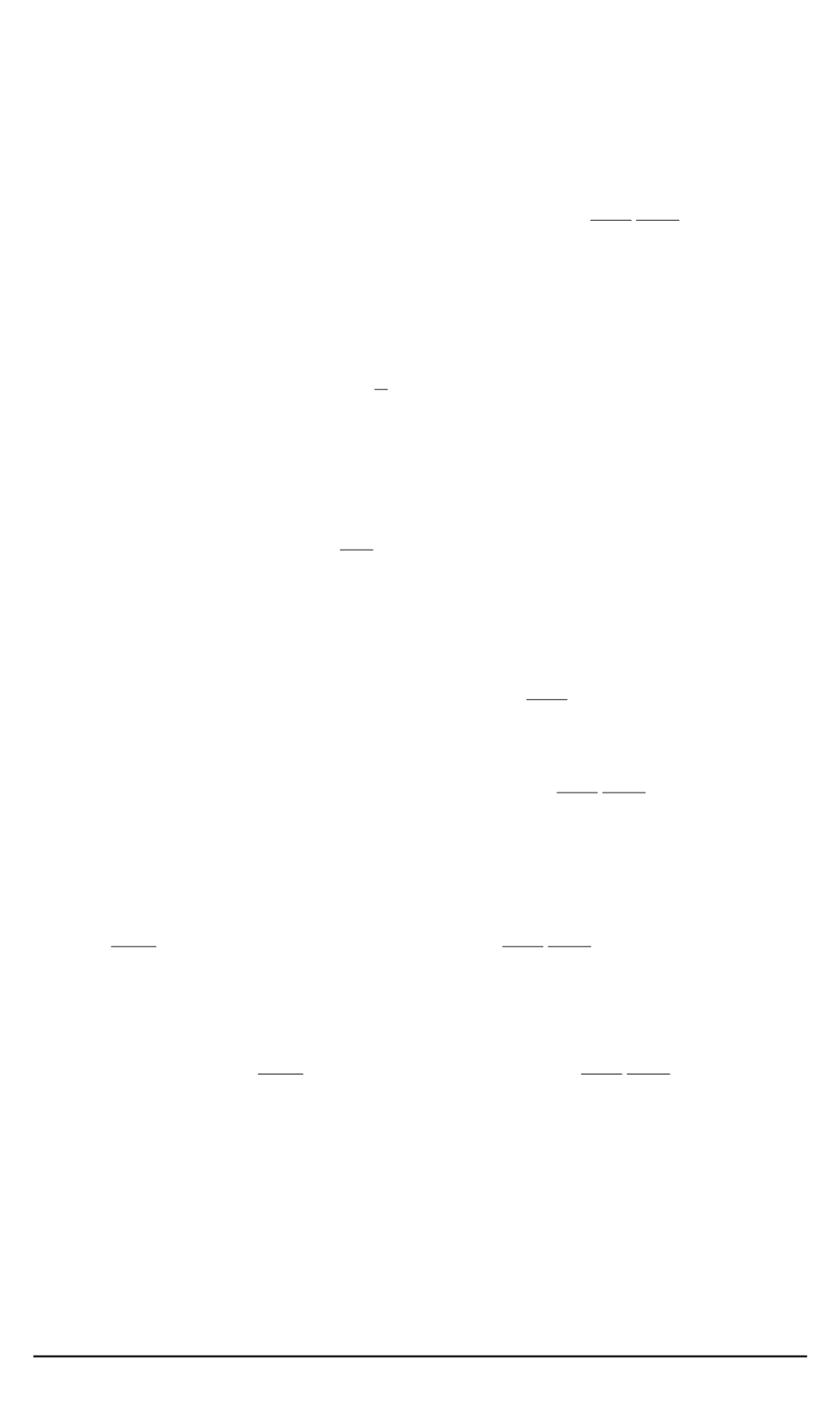
где
V
е
— объем конечного элемента;
dV
=
F dl
=
Fr dϕ
(
F
— площадь
поперечного сечения того или иного кольца).
В предположении, что плотность колецпостоянна (
ρ
=
const),
выражение для элемента матрицы масс запишется в виде
m
ij
=
ρFr
ϕ
2
ϕ
1
[
N
i
]
т
[
N
j
]
dϕ
=
ρFr
ϕ
2
ϕ
1
N
i
N
j
+
dN
i
dϕ
dN
j
dϕ
dϕ.
(7)
Аналогичную формулу для элемента матрицы масс можно полу-
чить, используя выражение для кинетической энергии
E
=
1
2
{
˙
δ
}
т
[
M
]
{
˙
δ
}
.
(8)
Для отдельного элемента кольца формулу кинетической энергии
можно представить как
E
=
ρF
2
ϕ
2
ϕ
1
( ˙
w
2
+ ˙
v
2
)
rdϕ.
Из формулы (4) следует, что
˙
v
=
6
i
=1
N
i
˙
δ
i
,
˙
w
=
−
6
i
=1
dN
i
dϕ
˙
δ
i
,
˙
v
2
=
6
i
=1
6
j
=1
N
i
N
j
˙
δ
i
˙
δ
j
,
˙
w
2
=
6
i
=1
6
j
=1
dN
i
dϕ
dN
j
dϕ
˙
δ
i
˙
δ
j
.
Таким образом,
E
=
ρF r
2
ϕ
2
ϕ
1
6
i
=1
6
j
=1
N
i
N
j
˙
δ
i
˙
δ
j
+
6
i
=1
6
j
=1
dN
i
dϕ
dN
j
dϕ
˙
δ
i
˙
δ
j
dϕ
=
=
ρF r
2
ϕ
2
ϕ
1
6
i
=1
6
j
=1
N
i
N
j
˙
δ
i
˙
δ
j
+
dN
i
dϕ
dN
j
dϕ
˙
δ
i
˙
δ
j
dϕ.
Сравнивая полученное выражение для кинетической энергии с
формулой (8), получаем то же выражение для элементов матрицы
масс (7).
Для однородного материала матрицу внутреннего демпфирования
можно вычислить через матрицу масс, умножая ее на
μ
/
ρ
, где
μ
— ко-
эффициент демпфирования. Таким образом, элементы матрицы демп-
26 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2010. № 4