пакета использовать теорию плоских круговых колецс учетом условий
их сопряжения.
Задача о изменении формы колецпод нагрузкой решается с по-
мощью дифференциальных уравнений упругих линий нерастяжимых
колец. Для каждого из колец уравнение имеет вид
EI
x
d
6
v
dϕ
6
+ 2
d
4
v
dϕ
4
+
d
2
v
dϕ
2
=
−
r
3
d
2
m
dϕ
2
+
m
−
r
4
dq
r
dϕ
+
q
t
,
(1)
где
v
— окружные перемещения;
ϕ
— угловая координата;
EI
x
— из-
гибная жесткость соответствующего кольца;
r
— радиус его средней
линии;
w
=
−
dv
dϕ
— радиальные перемещения;
θ
=
1
r
v
+
d
2
v
dϕ
2
—
угол поворота нормали;
q
r
— радиальная распределенная нагрузка;
q
t
— тангенциальная, или окружная распределенная нагрузка;
m
—
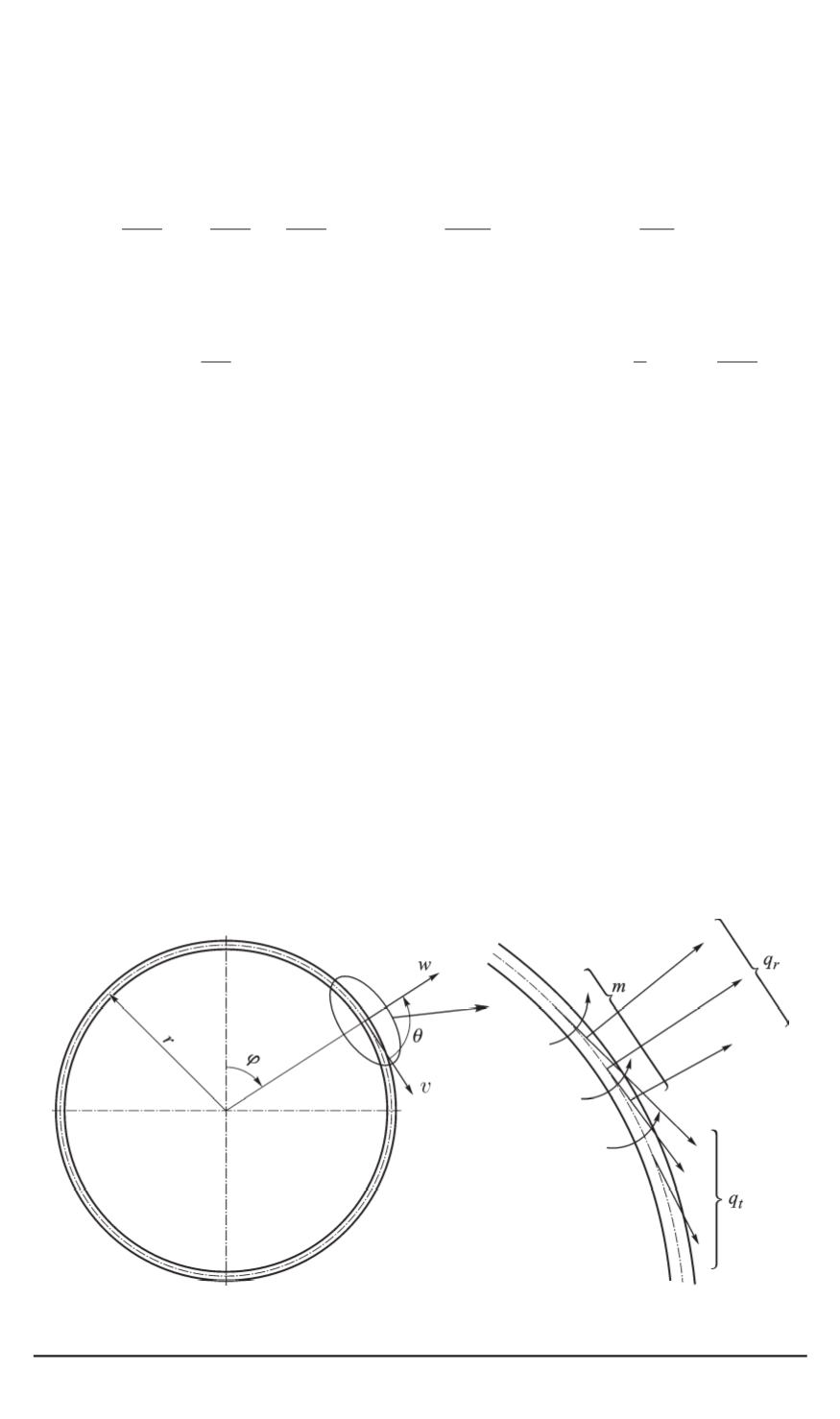
распределенный изгибающий момент (рис. 2).
Матрицы жесткости, масс и демпфирования конечного элемен-
та.
Решение динамической задачи системы из
k
колец(
k
= 1
,
2
,
3
. . .
—
число колецв пружинном пакете) предполагает решение матричного
дифференциального уравнения
[
M
]
{
¨
q
}
+ [
C
]
{
˙
q
}
+ [
K
]
{
q
}
=
{
P
}
,
(2)
где
[
M
]
— матрица масс;
[
C
]
— матрица сопротивления (демпфирова-
ния);
[
K
]
— матрица жесткости;
{
P
}
— вектор внешней нагрузки на
систему;
{
¨
q
}
,
{
˙
q
}
,
{
q
}
— векторы обобщенных ускорений, скоростей
и перемещений узлов конечных элементов.
Зная глобальные матрицы жесткости и масс системы, из решения
системы дифференциальных уравнений (2) в любой заданный момент
времени можно определить состояние системы в зависимости от дей-
ствия приложенных динамических сил.
Рис. 2. Кольцо пружинного пакета
24 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2010. № 4


