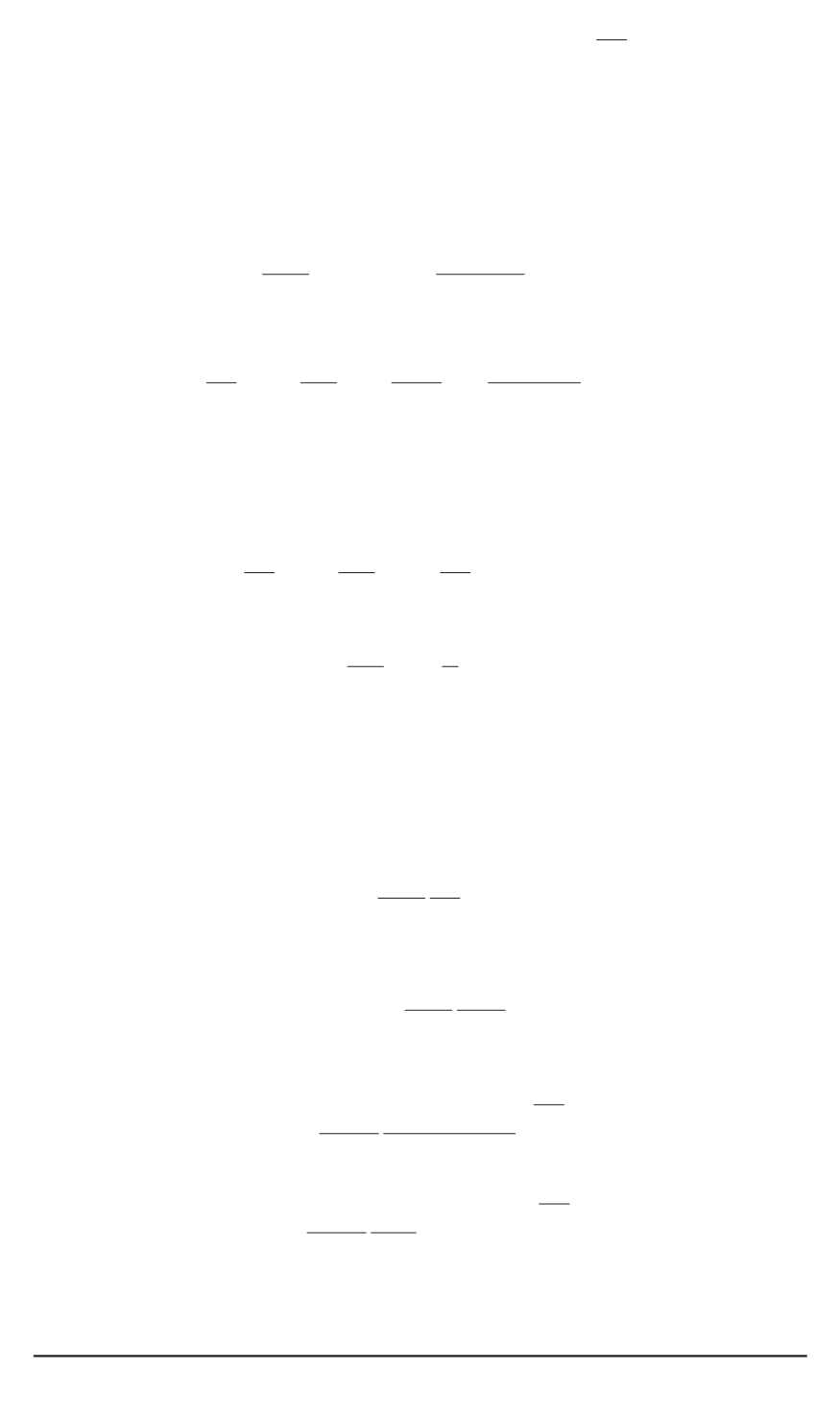
¯
N
4
=
N
(0) 1
−
c
(
n
−
1)
N
(0)
n
−
1
Ω
1
n
−
1
.
Функции
N
1
, N
3
,
¯
N
2
,
¯
N
4
определяют интегральные свойства релак-
сационного типа, а
N
2
, N
4
,
¯
N
1
,
¯
N
3
соответствуют возрастающим реше-
ниям, из которых два — катастрофические [3].
2. Осциллятор с одной степенью свободы.
Уравнение движения
осциллятора [4] с учетом уравнения состояния (1) имеет вид
d
2
N
dt
2
+
ω
2
0
N
+
c
d
(
BN
n
)
dt
= 0
,
где
ω
0
— собственная частота, или в операторной переменной
d
dω
βB
dN
dω
+
ω
2
0
N
βB
+
c
d
(
BN
n
)
dω
= 0
.
(3)
В основе приближенного исследования лежит предположение об
определении различных частных решений, удовлетворяющих отдель-
ным составляющим дифференциального уравнения. Например, ком-
бинация
d
dω
βB
dN
dω
+
c
d
dω
(
BN
n
) = 0
выполняется при
dN
dω
=
−
c
β
N
n
и имеет все свойства решения (2).
Отметим, что операторная переменная из-за различий в масшта-
бе реального времени позволяет исследовать огибающие вне связи с
периодическим движением.
Второе слагаемое
N
=
−
cβB
ω
2
o
d
dω
(
BN
n
)
при
B
=
B
0
=
const приводим к уравнению
N
=
−
cβB
ω
2
o
dN
n
dω
,
(4)
собственными функциями которого оказываются
N
=
N
(0) 1
−
n
−
1
n
ω
2
0
Ω
cB
2
0
N
(0)
n
−
1
1
n
−
1
при
n >
1
и
N
=
N
(0) 1 +
1
−
n
n
ω
2
0
Ω
cB
2
0
N
(0)
1
−
n
−
1
1
−
n
при
n <
1
.
С точностью до множителя перед
Ω
первая из этих функций совпа-
дает с
¯
N
4
, а вторая — с
¯
N
2
. Таким образом, сопряженные функции урав-
40 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2010. № 1