
А.А. Золотов, Э.Д. Нуруллаев
28
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. Машиностроение. 2016. № 5
Характер изменения математического
ожидания числа ошибок
M
(
i
) по циклам
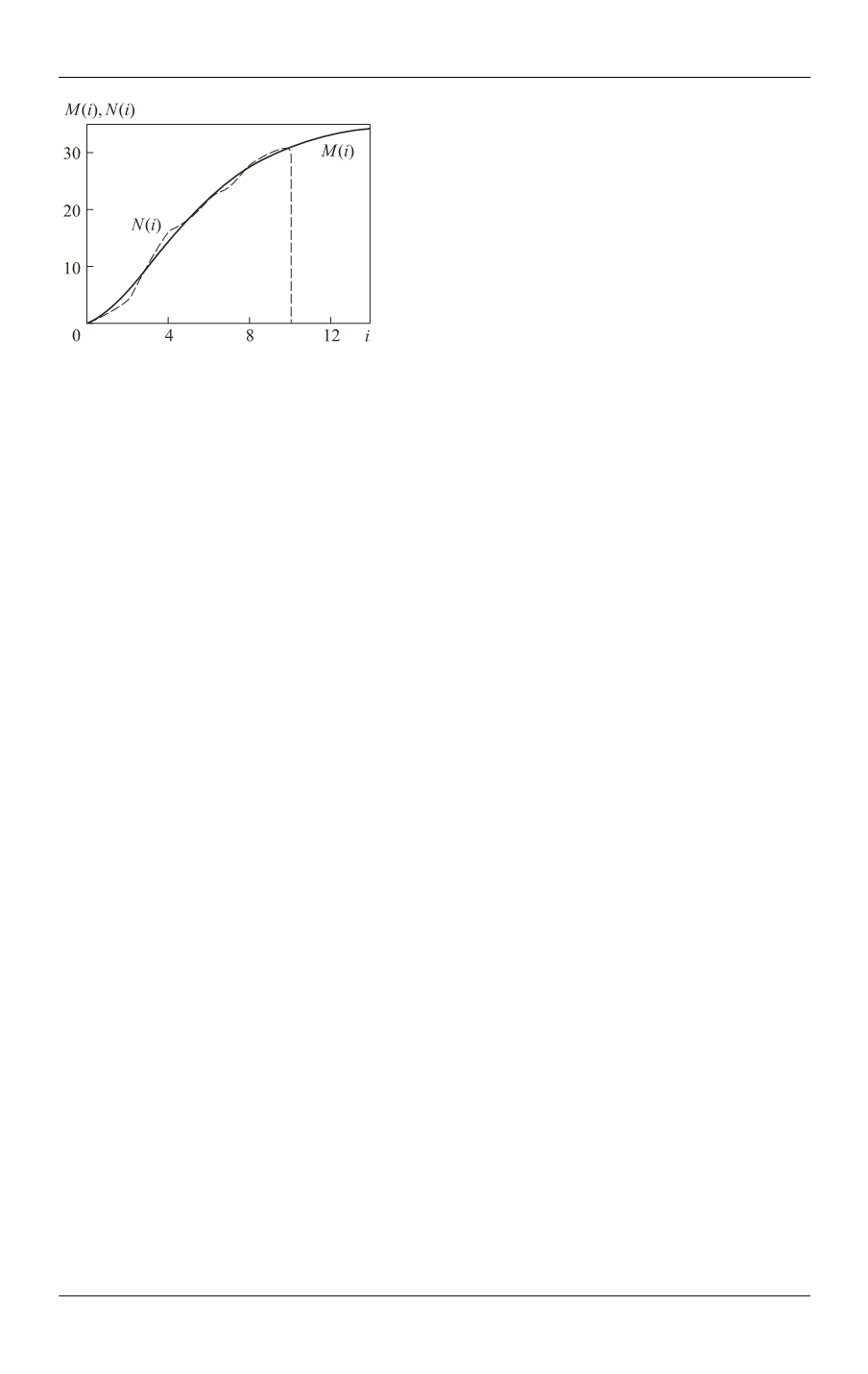
тестирования показан на рис. 3.
На графиках по оси абсцисс отложены
циклы тестирования, по оси ординат —
число выявленных ошибок. Реальное накоп-
ление ошибок представлено штриховой кри-
вой
N
(
i
). Обе кривые имеют слабо выражен-
ную
S
-образную форму. Как видно на графи-
ке, аппроксимирующая кривая хорошо
согласуется с опытными данными.
Прогнозирование надежности ПО на
основе численной модели.
Рассмотренная
задача также может быть решена с помощью
численной модели, позволяющей снять до-
пущения аналитической модели. Для оценки числа отказов используем алгоритм,
представленный в работе [5]. Программа расчетов по указанному алгоритму при-
ведена на рис. 4. При расчетах принимают
0,
что соответствует режиму «вы-
жигания» отказов, задают значения исходных параметров
, ,
0,0
.
M
Искомые
параметры, оцениваемые программой расчетов после
n
циклов тестирования,
определяются треугольной матрицей
( )
M n
, которая является функцией количе-
ства циклов тестирования. В этой матрице нулевая строка соответствует значению
0,0
,
M
характеризующему исходное число анализируемых критических элементов
системы,
i
-й строке и
j
-му столбцу матрицы соответствует элемент
,
,
i j
M
характе-
ризующий число элементов, функционирующих на
i
-м цикле тестирования и за-
мененных на новые на
j
-м цикле тестирования. Число ошибок на
i
-м цикле тести-
рования выводится отдельно как диагональный элемент матрицы
,
( ) .
i i
M n
Для
проведения расчетов по предлагаемой методике необходимо оценить параметры
модели, согласующиеся с результатами тестирования. Расчеты параметров
, ,
0,0
M
выполняют по методу наименьших квадратов, согласно которому значения
исходных параметров должны обеспечивать минимальную сумму квадратов от-
клонений зафиксированного числа ошибок от прогнозируемых на каждом цикле
тестирования, т. е. минимум критериальной функции
L
:
2
0
0
ˆ
( , ,
) ,
k
k
k
L M M M
(3)
где
ˆ
k
M
— число ошибок, зафиксированных на
k
-м цикле тестирования;
0
0,0
( , ,
)
k
M M
— прогнозируемое число ошибок на
k
-м цикле тестирования,
рассчитываемое по алгоритму, представленному ранее.
В дальнейшем, учитывая, что число ошибок на всех циклах пропорцио-
нально
0,0
,
M
переходим к рассмотрению относительного числа ошибок:
Рис. 3.
Зависимости изменения сгла-
живающей
( )
M i
(сплошная кривая) и
экспериментальной
( )
N i
(штрихо-
вая) кривых от количества циклов
тестирования
















