
Прогнозирование числа отказов программного обеспечения космических аппаратов
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. Машиностроение. 2016. № 5
27
где
1
1
2
2
1
1
1
1
(
)
Ф( )
(
)
1 (1 )
.
[( 1
)
(1 )
]
k
k
n
n
k
k
bt
bt
n
k
k
bt
bt
k r
n
bt
bt
k
k
k
t e
t e
b
y y
e
bt e
bt e
bt e
Для иллюстрации работоспособности предлагаемой методики рассматри-
ваем модельный пример, представленный в работе [7]. Предполагаем, что за
10 циклов тестирования была выявлена 31 ошибка. Далее приведены результаты
по каждому циклу тестирования:
n
0
= 0;
n
1
= 2;
n
2
= 4;
n
3
= 10;
n
4
= 16;
n
5
= 18;
n
6
= 22;
n
7
= 24;
n
8
= 28;
n
9
= 30;
n
10
= 31, где
n
i
— накопленное число ошибок, со-
ответствующее
i
-му циклу тестирования.
Искомые значения
b
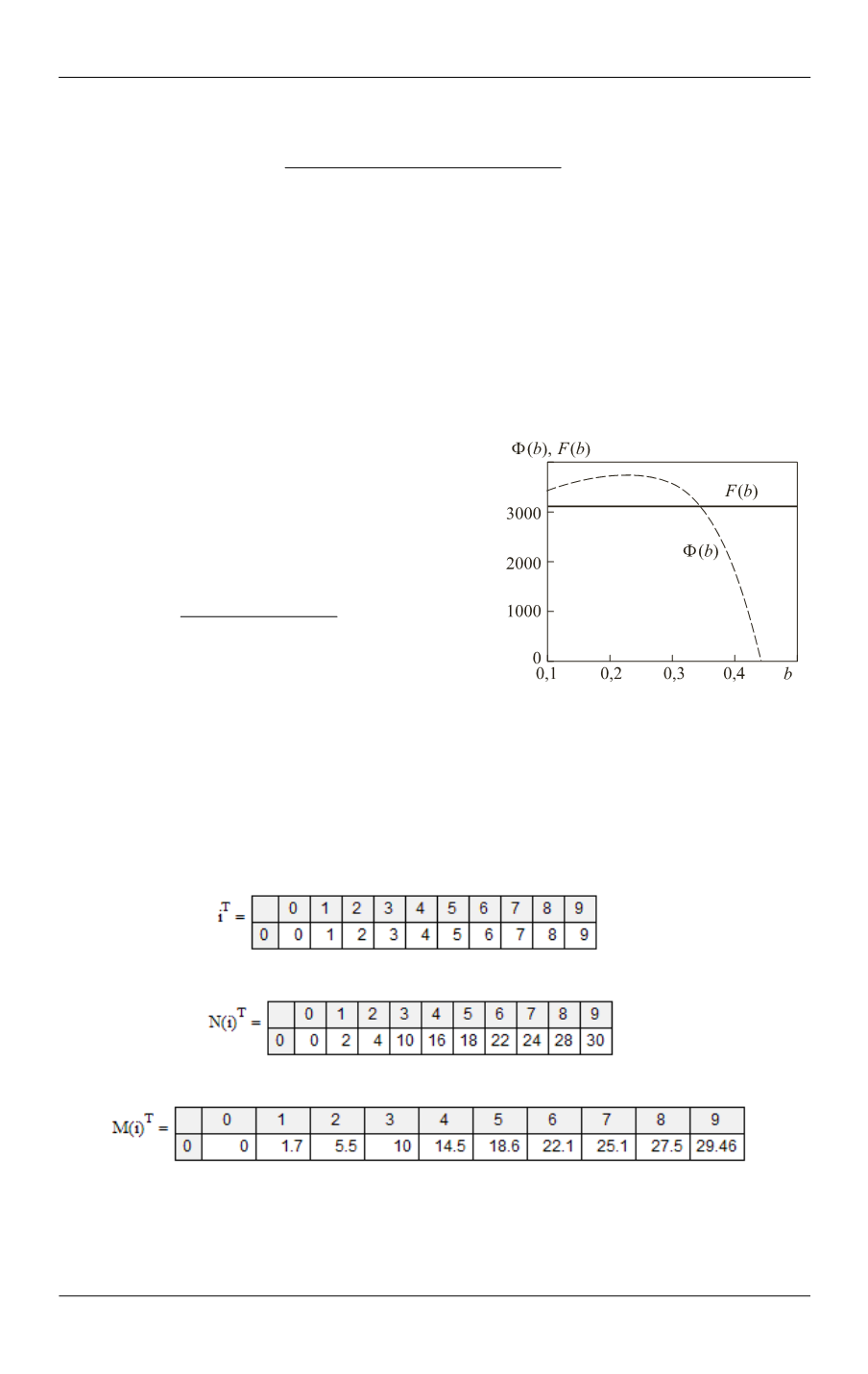
оценены графически при выполнении условия (рис. 1)
2
Ф( ).
n n
y t
b
(2)
Как следует из графика, условие (2) удо-
влетворяется при значении
b
= 0,345. Далее
по соотношению (1) оценивают значение па-
раметра
a
:
36,1.
1 (1 )
n
n
bt
n
y
a
bt e
Зная
a
и
b
, можно найти распределение
прогнозируемых значений числа ошибок
( )
M i
по циклам тестирования
i
:
( )
1 (1 )
.
ib
M i a
bi e
Результаты расчета приведены на рис. 2.
Рис. 2.
Распределение расчетных оценок
M
(
i
) и реального накопления ошибок
N
(
i
)
по циклам тестирования
i
Рис. 1.
Зависимости изменения
функций
Ф( )
b
(штриховая кривая)
и
( )
F b
(сплошная) от параметра
b
















