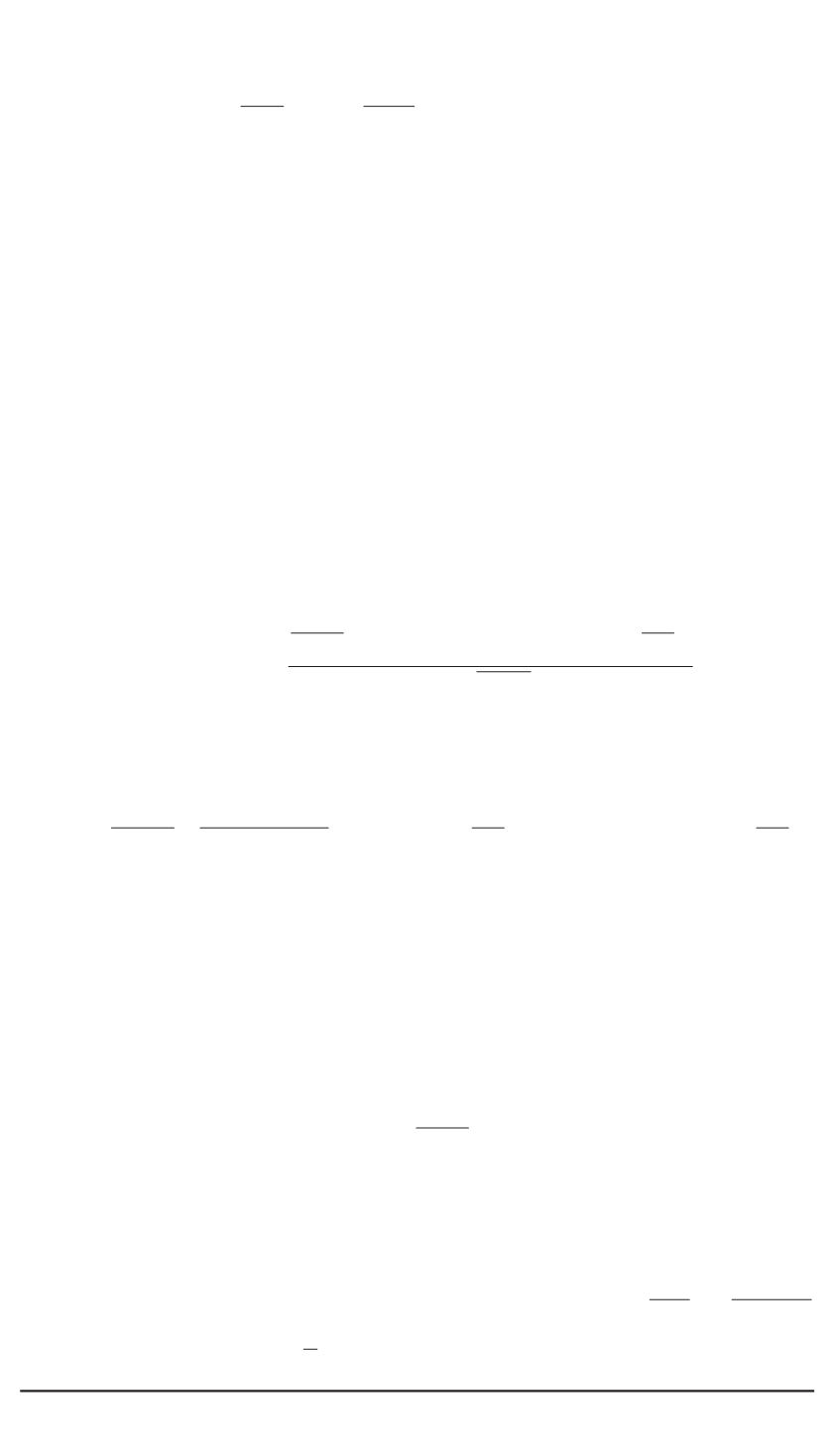
М
0
, угловой коэффициент которой является производной
d
Ω
0
dy
0
= lim
ΔΩ
0
Δ
y
0
при
Δ
y
0
→
0
.
Положение этой касательной в стружке определитсяпри под-
становке в формулу (17) вместо отношения
ВВ
1
/
АВ
производной
d
Ω
0
/dy
0
. Нетрудно показать, что касательнаяк кривой
Ω(
y
)
остается
касательной и к деформированной кривой
Ω
1
(
y
1
)
в стружке. Действи-
тельно, если на рис. 3 точки
М
1
и
М
11
кривой
Ω
1
(
y
1
)
соответствуют
точкам
М
0
и
М
01
в срезаемом слое, то при
Δ
y
0
→
0
как секущая
М
0
М
01
→
0
, так и
М
1
М
11
→
0
. Предельные положенияэтих секущих
и будут касательными к кривым
Ω(
y
)
и
Ω
1
(
y
1
)
в соответствующих
точках
М
0
и
М
1
.
Таким образом, если функция
Ω =
f
(
y
)
на исследуемом участке
0
≤
y
≤
a
(
a
— толщина срезаемого слоя) является дифференцируемой,
то каждой точке кривой
Ω(
y
)
соответствует определенное значение
угла
δ
(
y
) = arccos
1
sin
β
+ tg(
β
−
γ
) cos
β
−
sin
β
d
Ω
dy
G
(
y
)
.
(21)
Здесь через
G
(
y
)
обозначено
G
(
y
) =
1
sin
2
β
+
1
cos
2
(
β
−
γ
)
(cos
β
−
sin
β
d
Ω
dy
)
2
+2 tg(
β
−
γ
) ctg
β
−
d
Ω
dy
.
Выражение (21) представляет собой семейство направлений, кото-
рые составляют касательные к кривой
Ω(
y
)
по отношению к плоскости
сдвига после деформации в процессе стружкообразования.
Следует отметить, что каждаяточка
М
(
y,
Ω)
кривой
Ω(
y
)
после
деформации определяется в координатной системе
Ω
1
0
1
y
1
новым зна-
чением абсциссы
y
1
, которое зависит от угла сдвига
β
и составля ет
y
1
=
y
sin
β
.
(22)
Необходимость пересчета положениясоответствующих точек в
срезаемом слое и стружке можно исключить, если зависимости
Ω(
y
)
и
Ω
1
(
y
1
)
представить как функции новой переменной
η
, записанной в
безразмерном виде. Пусть
η
=
y/a
(0
≤
η
≤
1)
;
η
1
=
y
1
OA
=
y
1
sin
β
a
или c учетом (22)
η
1
=
y
a
=
η
.
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2012. № 3 109