
и плотность теплового потока в узле
n
по уравнению
q
n
=
1
2Δ
t
cρ
n
−
1
L
n
−
1
T
n
−
T
n
−
1
−
λ
n
−
1
L
(
T
n
−
1
−
T
n
)
.
(17)
Вычисления по шагам по времени необходимо продолжать до вы-
полнения условий периодичности. Завершение итерационного процес-
са осуществляется при выполнении условия
q
ls
=
q
ns
, где
q
ls
,
q
ns
—
средние за период цикла
θ
значения плотностей тепловых потоков на
тепловоспринимающей и теплоотдающей поверхностях теплометри-
ческого элемента (узлы
1
и
n
).
На рис. 5 приведен результат решения ОЗТ при отсутствии нагара
на поверхности защитного слоя, а на рис. 6 и 7 — результаты решения
ОЗТ для датчика с нагаром. При этом на рис. 6 приведено решение
ОЗТ для датчика со слоем нагара толщиной 0,05 мм, а на рис. 7 —
решение той же задачи, но в предположении отсутствия слоя нагара
на поверхности защитного слоя. Отметим, что толщину слоя нагара
можно определить по методу, предложенному в [4, 5].
Полученные результаты показывают высокую демпфирующую
способность отложений сажи на поверхностях датчика и существен-
ную ошибку, возникающую при восстановлении плотности теплового
потока по показаниям датчика при наличии на его поверхности не-
контролируемых отложений, структура и свойства которых могут
существенно изменяться на различных режимах работы двигателя.
Заключение.
Разработанный метод решения внешних обратных
нестационарных задач теплопроводности для многослойных структур,
и созданное соответствующее программное обеспечение предназна-
чены для исследования локального теплообмена в камерах сгорания
ДВС. Полученные в настоящей работе результаты, а также проведен-
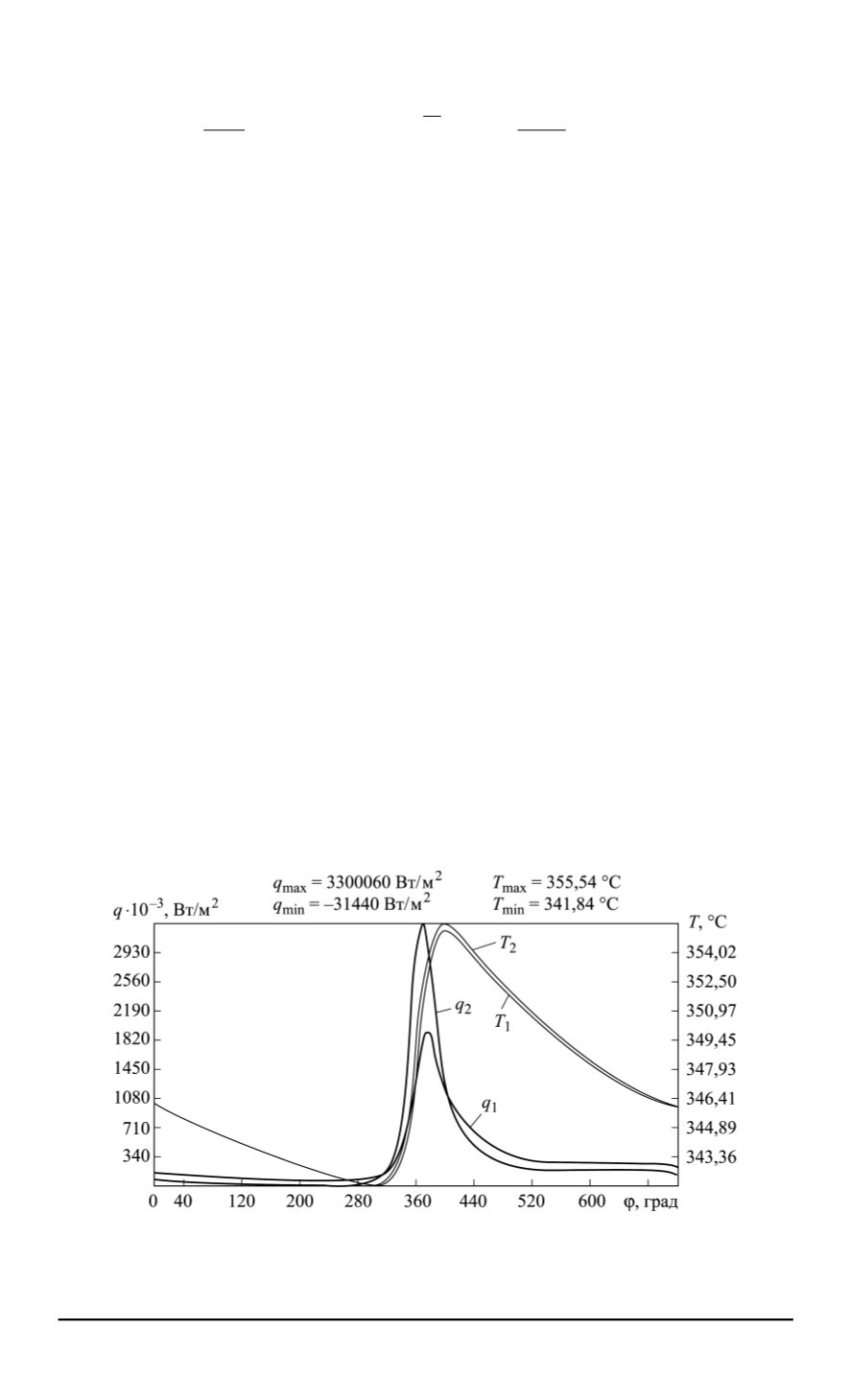
Рис. 5. Восстановленная плотность теплового потока на поверхности защитного
слоя (
q
2
) и поверхности теплометрического элемента (
q
1
) и колебания тем-
пературы поверхностей защитного слоя (
T
2
) и теплометрического элемента (
T
1
)
76 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2016. № 1
















