
для неоднородной пластины (теплометрический элемент с защитным
слоем):
∂T
∂t
=
a
1
∂
2
T
∂X
2
при
X
∈
(0
, l
1
)
,
∂T
∂t
=
a
2
∂
2
T
∂X
2
при
X
∈
(
l
1
, l
2
)
,
(1)
T
(
X,
0) =
G
(
X
)
, T
(
l
1
, t
) =
F
(
t
)
,
λ
∂T
(
−
l
2
, t
)
∂X
=
q
(
t
)
, λ
1
∂T
(0
, t
)
∂X
=
λ
2
∂T
(0
, t
)
∂X
,
(2)
где
l
1
— толщина теплометрического элемента;
l
2
— толщина защитного
слоя;
а
1
,
λ
1
— коэффициенты температуропроводности и теплопровод-
ности теплометрического элемента;
а
2
,
λ
2
— коэффициенты темпера-
туропроводности и теплопроводности защитного слоя.
Такая задача соответствует случаю двуслойной пластины (тепло-
метрический элемент и защитный слой датчика теплового потока).
В условиях рабочего процесса двигателя, особенно дизеля, где гете-
рогенный процесс сгорания сопровождается выделением сажи [6, 7],
защитный слой датчика покрывается сажей, имеющей низкую те-
плопроводность, поэтому целесообразно рассматривать трехслойную
структуру. Для многослойных пластин в принципе можно попытать-
ся построить аналитическое решение и свести задачу к задаче с
однородными граничными условиями. Однако математические труд-
ности, возникающие при этом, очевидны. Поэтому имеет смысл ис-
пользовать для решения задачи восстановления плотности нестаци-
онарного теплового потока на поверхности многослойной пластины
численный метод решения, позволяющий получить решение для мно-
гослойных структур. Рассмотрим в качестве примера трехслойную
структуру (пластину), состоящую из теплометрического элемента,
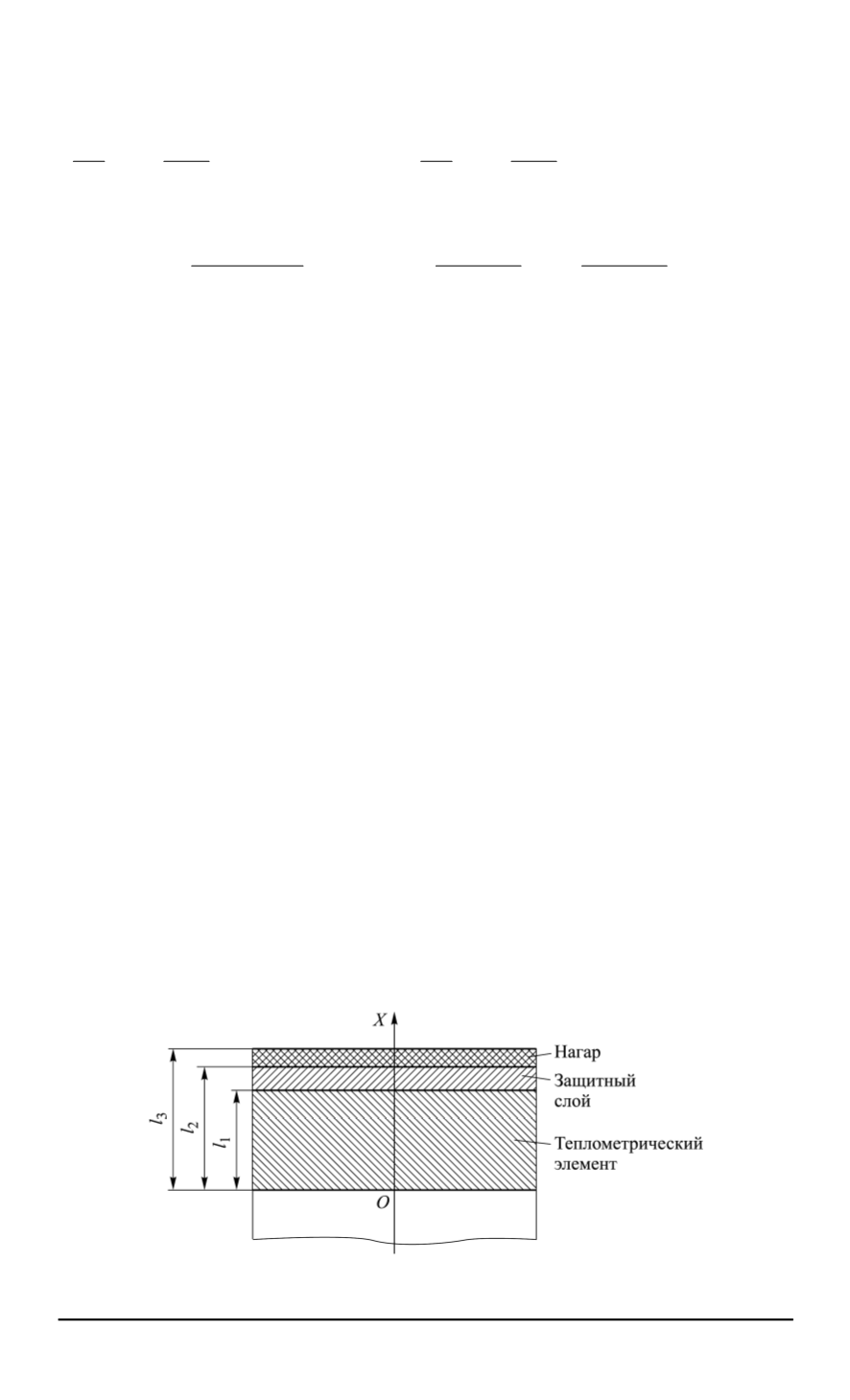
защитного слоя и слоя сажи (рис. 2).
Необходимо оценить плотность теплового тока на поверхностях
теплометрического элемента, поверхностях контакта защитного слоя
и слоя сажи, имея значения колебаний температур поверхностей теп-
лометрического элемента в пределах одного цикла двигателя. Пред-
Рис. 2. Схема расчета датчика теплового потока, покрытого слоем нагара
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение” 2016. № 1 71
















