
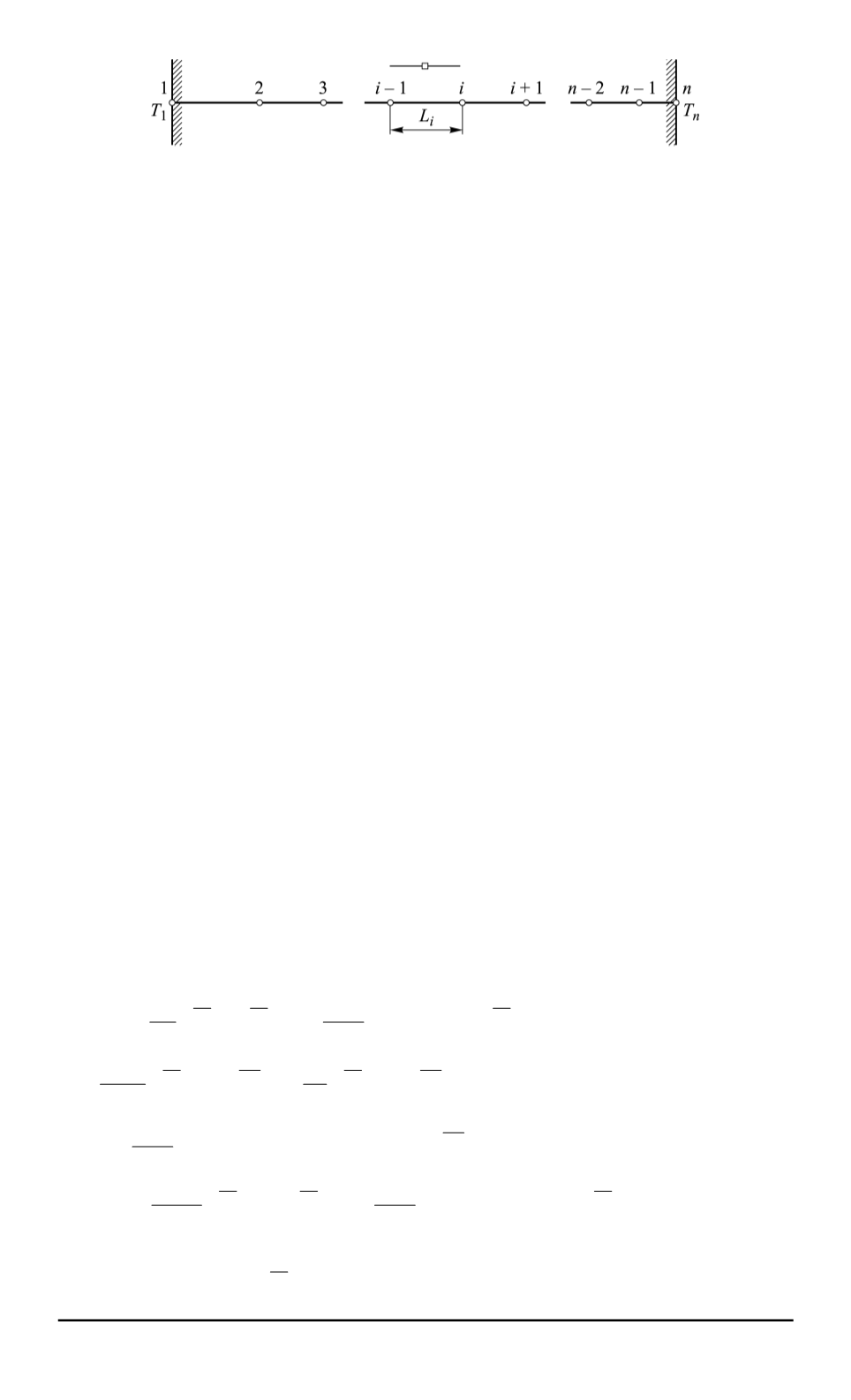
Рис. 3. Конечно-элементная модель теплометрического элемента
Это условие может быть достигнуто методом установления. Для уско-
рения процесса установления в качестве начального условия целе-
сообразно задавать в рассматриваемых подобластях начальное рас-
пределение температуры, соответствующее условному стационарному
режиму (рассчитав начальное распределение температуры в каждой
подобласти с заданием осредненных по времени граничных условий).
Для решения ОЗТ на каждом этапе используем модифицированный
вариант МКЭ–МКО, при этом при решении ОЗТ на первом этапе це-
лесообразно применить явную схему аппроксимации ОЗТ, а на втором
этапе неявную схему.
Решение ОЗТ для теплометрического элемента.
Область теп-
лометрического элемента аппроксимируем одномерными конечными
элементами (рис. 3), в пределах которых распределение температуры
имеет вид линейной зависимости
T
= [
N
i
, N
j
]
∙
T
i
T
j
,
(7)
где
N
i
, N
j
— функция формы;
Т
i
,
Т
j
— значения температуры в узлах
i
и
j
.
Узлы конечно-элементной модели распределим в области со сгу-
щением от узла
1
(
Х
= 0
) к узлу
n
, учитывая нарастание амплитуды
колебания температуры при приближении к нагреваемой поверхности
теплометрического элемента. Каждому элементу поставим в соответ-
ствие значения теплофизических характеристик (
λ
,
cρ
) для учета их
зависимости от температуры. Поставив в соответствие каждому узлу
контрольный объем и выполнив стандартные операции МКО, получим
дискретный аналог уравнения теплопроводности и соответствующие
конечно-разностные уравнения:
q
1
+
λ
1
L
1
T
2
−
T
1
=
1
2Δ
t
cρ
1
L
1
T
1
−
T
1
, i
= 1;
λ
i
−
1
L
i
−
1
T
i
−
1
−
T
i
+
λ
i
L
i
T
i
+1
−
T
i
=
=
1
2Δ
t
(
cρ
i
−
1
L
i
−
1
+
cρ
i
L
i
)
T
i
−
T
i
, i
= 2
, . . . , n
−
1;
q
n
+
λ
n
−
1
L
n
−
1
T
n
−
1
−
T
n
=
1
2Δ
t
cρ
n
−
1
L
n
−
1
T
n
−
T
n
, i
=
n,
(8)
где
L
i
— длина элемента;
Δ
t
— шаг по времени, выбираемый по усло-
вию устойчивости;
T
— значение температуры на предыдущем вре-
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение” 2016. № 1 73
















