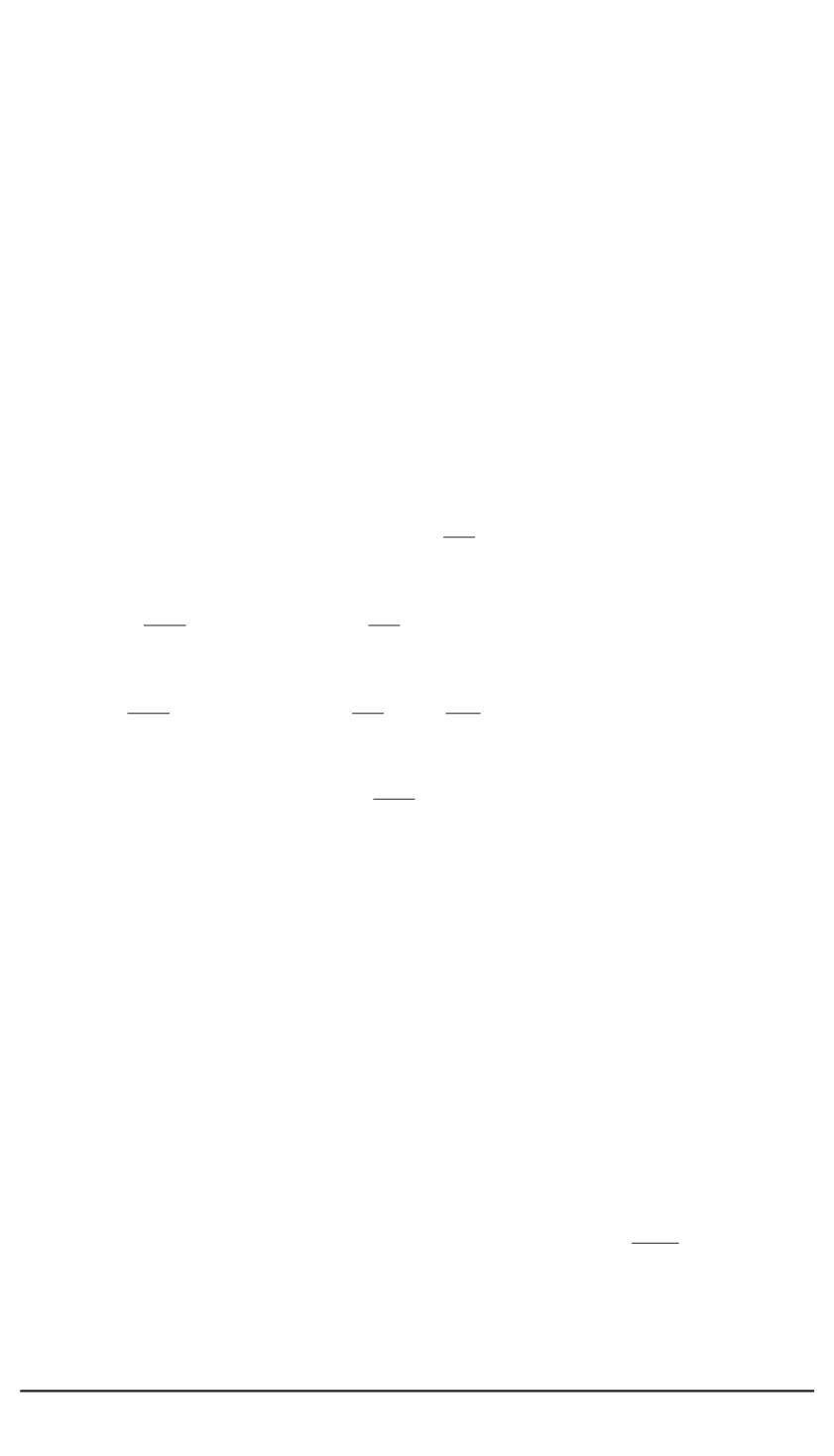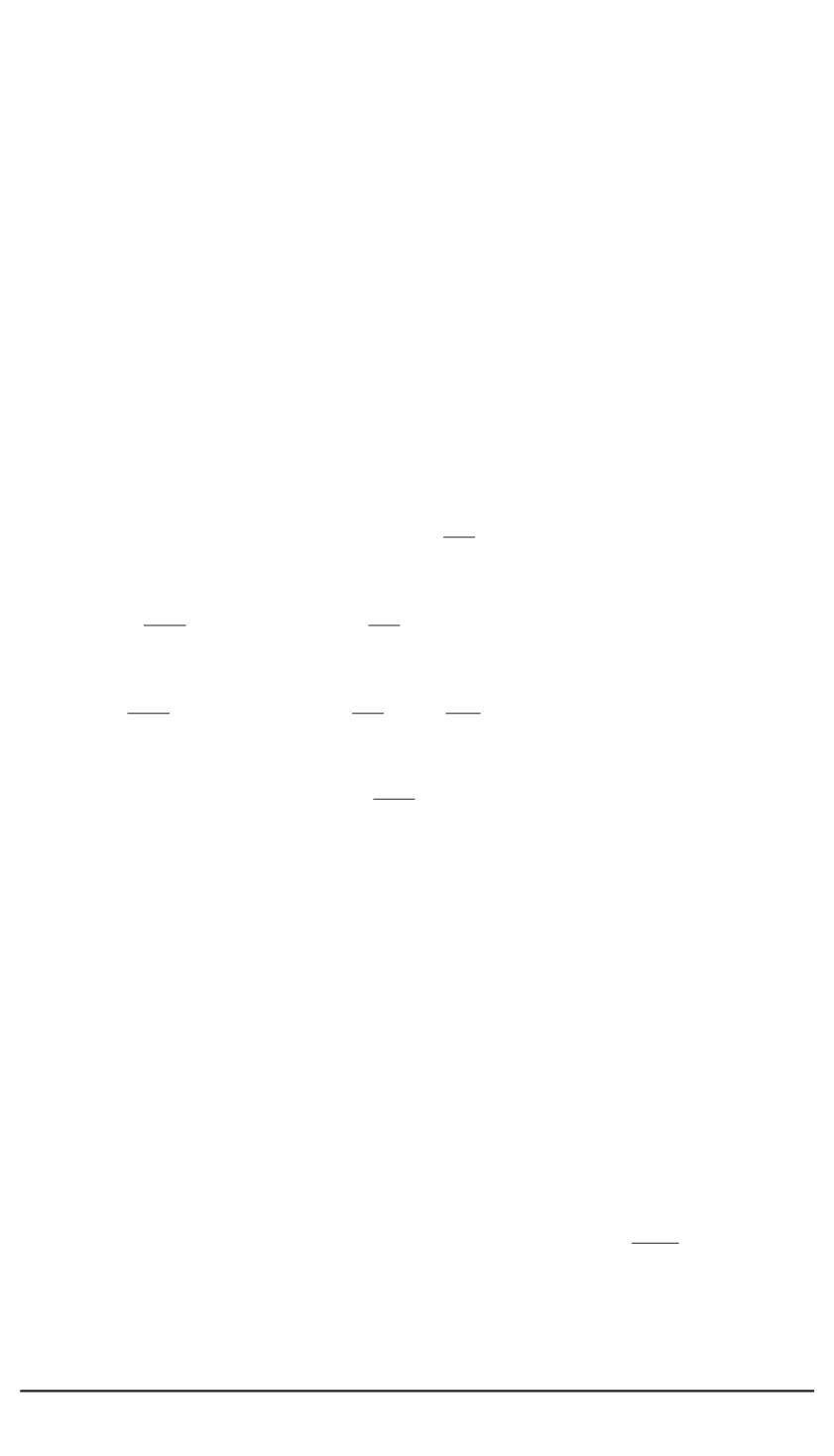
статье рассмотрена соответствующая спектральная задача – задача о
собственных колебаниях.
Постановка задачи.
Пусть несжимаемая жидкость, находящаяся
в потенциальном поле массовых сил с интенсивностью
j
=
−
gne
3
,
частично заполняет произвольный сосуд и вытекает через поверхность
слива с постоянной скоростью (
n, e
3
— перегрузка и орт оси
Ox
3
с
началом на поверхности слива).
Обозначим через
Q
область, занимаемую жидкостью,
S
— твердую
стенку бака, которую будем считать кусочно-гладкой, через
Γ
1
,
Γ
2
—
свободную поверхность и поверхность слива соответственно.
Предполагая движения во всей области занимаемой жидкостью по-
тенциальными и удовлетворяющими условию непротекания на смачи-
ваемой поверхности
S
, сформулируем краевую задачу для нахождения
потенциала смещений — функции
χ
(
x, t
)
(
x
=
x
1
, x
2
, x
3
):
Δ
χ
= 0
в
Q,
∂χ
∂n
= 0
на
S
;
(1)
∂
2
χ
∂t
2
+
v
1
(
x
1
, x
2
)
· ∇
∂χ
∂t
+
gw
·
n
1
=
f
1
(
t
)
на
Γ
1
;
(2)
∂
2
χ
∂t
2
+
v
2
(
x
1
, x
2
)
· ∇
∂χ
∂t
+
γ
∗
∂w
∂t
·
n
2
=
f
2
(
t
)
на
Γ
2
;
(3)
w
i
=
w
0
i
(
x
1
, x
2
)
,
∂w
i
∂t
=
v
0
i
(
x
1
, x
2
)
, i
= 1
,
2
,
где
v
k
(
x
1
, x
2
)
,
k
= 1
,
2
, — вертикальные компоненты значений невозму-
щенной скорости жидкости на свободной поверхности
Γ
1
и поверхно-
сти слива
Γ
2
соответственно;
γ
∗
=
ξ
|
V
0
Σ
|
— обобщенный коэффициент
сопротивления;
ξ
– коэффициент сопротивления заборного устрой-
ства;
v
Σ
(0) =
V
0
Σ
— вектор среднeй скорости невозмущенной жидкости
на поверхности перераспределения топлива
Γ
2
;
w
(
x, t
) =
∇
χ
(
x, t
)
—
векторное поле смещений частиц жидкости; остальные обозначения
соответствуют обозначениям работы [6].
Определение.
Будем называть нормальными (собственными) дви-
жениями гидромеханической системы (1)–(3) движения, подчиненные
решениям вида
w
(
x, t
) =
u
(
x
) exp(
−
λt
)
, χ
(
x, t
) =
ϕ
(
x
) exp(
−
λt
)
,
(4)
где
u
(
x
)
, ϕ
(
x
)
— амплитудные функции;
λ
=
λ
∗
/ gl
−
1
(
λ
∗
— ком-
плексный коэффициент затухания). Подставив представление (4) в
(1)–(3) и положив
f
1
(
t
)
, f
2
(
t
) = 0
, придем к задаче о собственных
колебаниях, записанной в безразмерном виде,
32 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2012. № 3