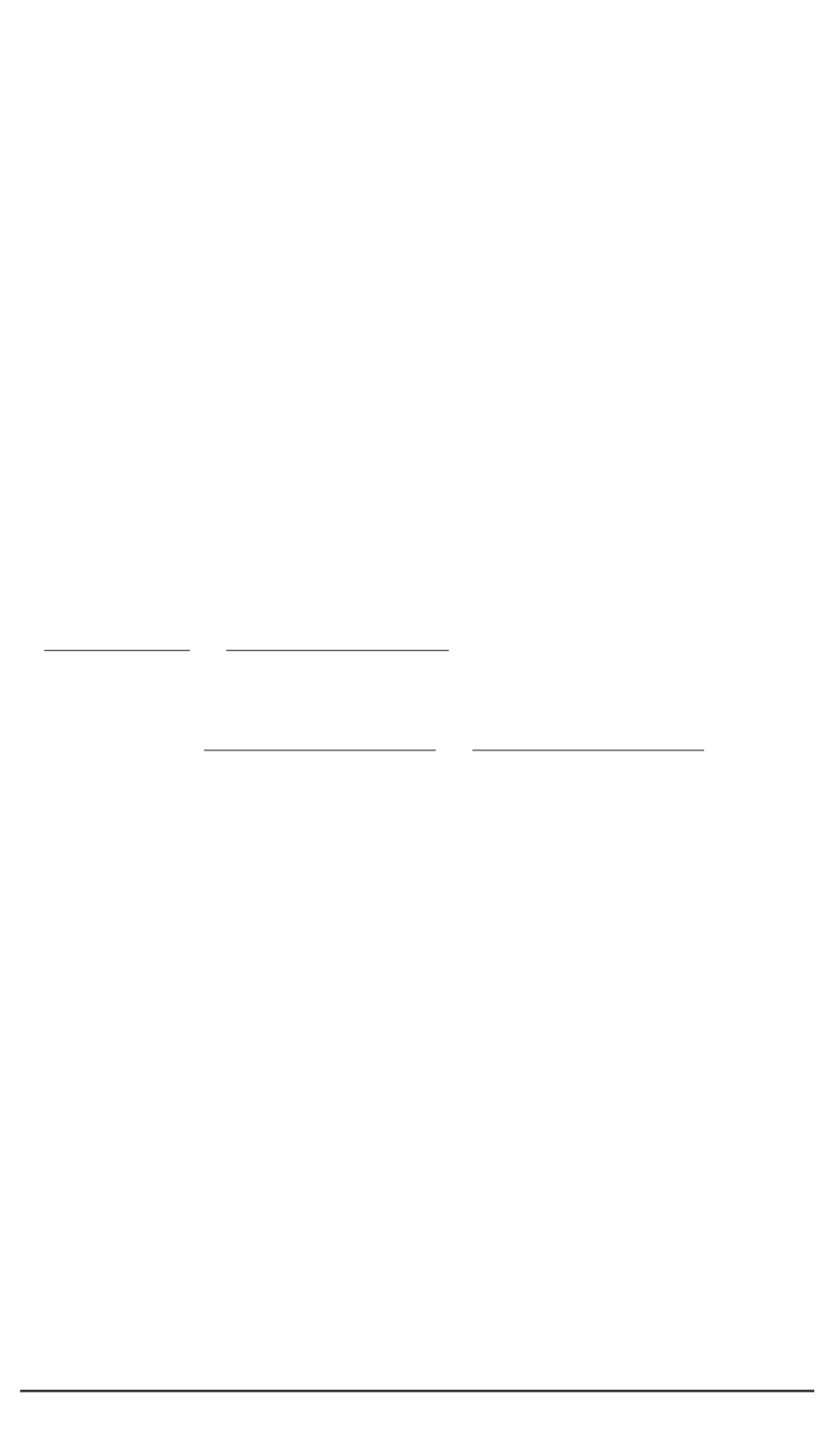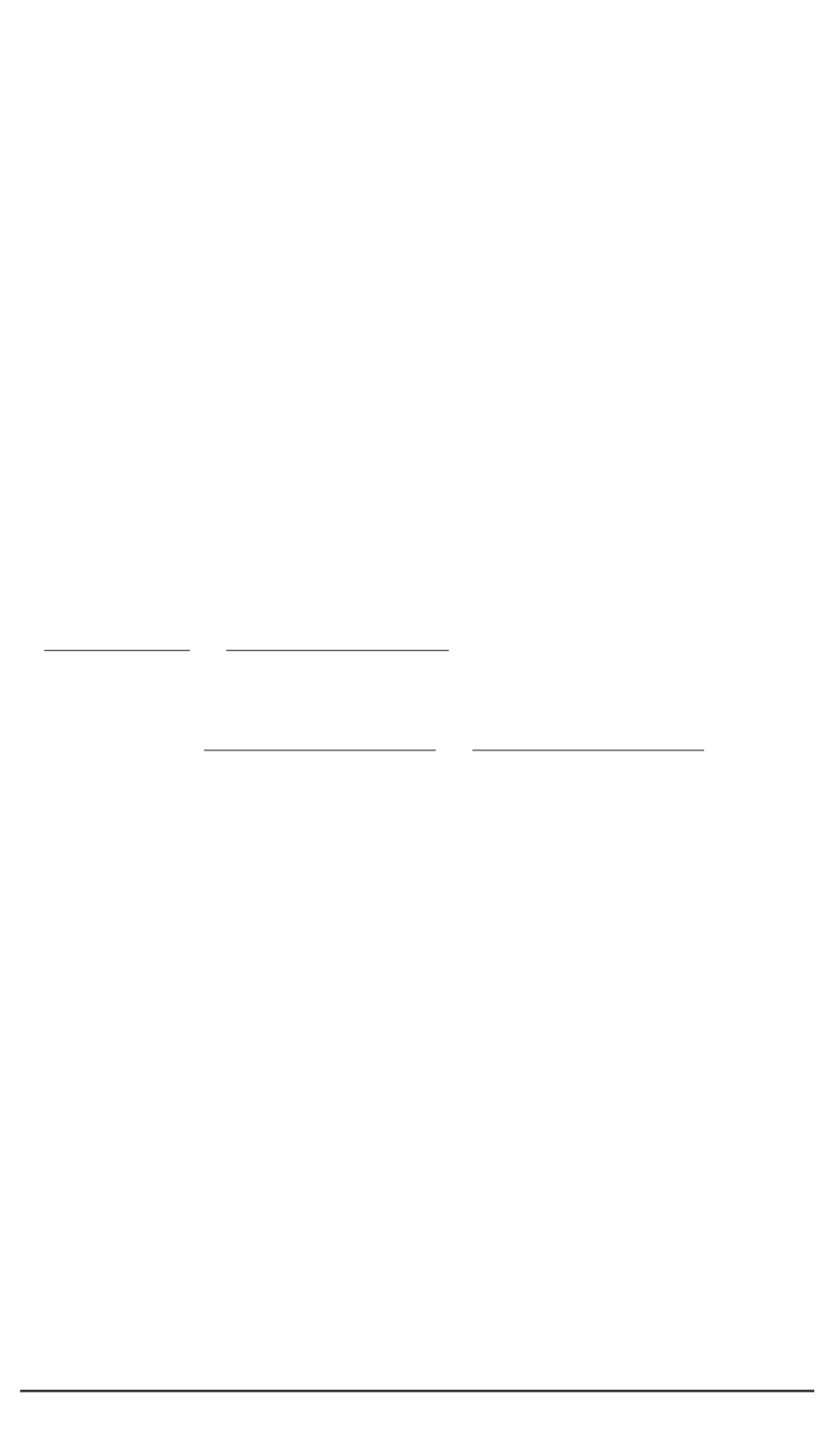
G
=
⎛
⎜⎜⎜⎜⎝
ρυ
ρυu
−
σ
yx
ρυυ
+
P
−
σ
yy
ρυw
−
σ
yz
(
ρE
+
P
)
υ
−
uσ
yx
−
υσ
yy
−
wσ
yz
+
Q
y
⎞
⎟⎟⎟⎟⎠
;
H
=
⎛
⎜⎜⎜⎜⎝
ρw
ρwu
−
σ
zx
ρwυ
−
σ
zy
ρww
+
P
−
σ
zz
(
ρE
+
P
)
w
−
uσ
zx
−
υσ
zy
−
wσ
zz
+
Q
z
⎞
⎟⎟⎟⎟⎠
.
Газовая среда, натекающая на ГЛА, рассматривается как совершен-
ный газ с показателем адиабаты
γ
= 1
,
4
.
Для численного решения уравнений Навье–Стокса и дифференци-
альной двухпараметрической
q
−
ω
-модели вихревой вязкости Кокли
использован явный интегроинтерполяционный метод, применение ко-
торого для уравнений (2) на равномерной декартовой сетке приводит
к следующей конечно-разностной схеме:
Q
n
+1
i,j,k
−
Q
n
i,j,k
Δ
t
+
F
n
i
+1/2
,j,k
−
F
n
i
−
1/2
,j,k
Δ
x
+
+
G
n
i,j
+1/2
,k
−
G
n
i,j
−
1/2
,k
Δ
y
+
H
n
i,j,k
+1/2
−
H
n
i,j,k
−
1/2
Δ
z
= 0
,
(3)
где
Δ
x
,
Δ
y
и
Δ
z
— шаги сетки в направлениях осей
х
,
y
и
z
. Тройной
целый нижний индекс
(
i, j, k
)
обозначает значения сеточных функций,
отнесенные к центрам соответствующих трехмерных дискретных ре-
гулярных ячеек, а полуцелые нижние индексы относятся к значениям
функций на границах ячеек. При численном решении гиперболиче-
ской (“невязкой”) части уравнения величины с полуцелыми индексами
Q
i
±
1/2
,j,k
,
Q
i,j
±
1/2
,k
,
Q
i,j,k
±
1/2
находятся из решения соответствующих
задач Римана [14] (для построения численной схемы следует решать
задачу Римана на каждой из границ дискретных ячеек). Векторы пото-
ков, которые входят в уравнение (2), определяются следующим обра-
зом:
F
n
i
±
1/2
,j,k
=
F Q
i
±
1/2
,j,k
,
G
n
i,j
±
1/2
,k
=
G Q
i,j
±
1/2
,k
, H
n
i,j,k
±
1/2
=
H Q
i,j,k
±
1/2
.
Для нахождения потоковых величин
F
HLL
i
±
1/2
,j,k
,
G
HLL
i,j
±
1/2
,k
,
H
HLL
i,j,k
±
1/2
применяется TVD-монотонизированный вариант метода Хартена–
Лакса–Ван Лира (HLL) (см., например, [14]). Функциональный вид
выражений для векторов потоков
F
n
i
±
1/2
,j,k
,
G
n
i,j
±
1/2
,k
,
H
n
i,j,k
±
1/2
осно-
22 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2012. № 3