
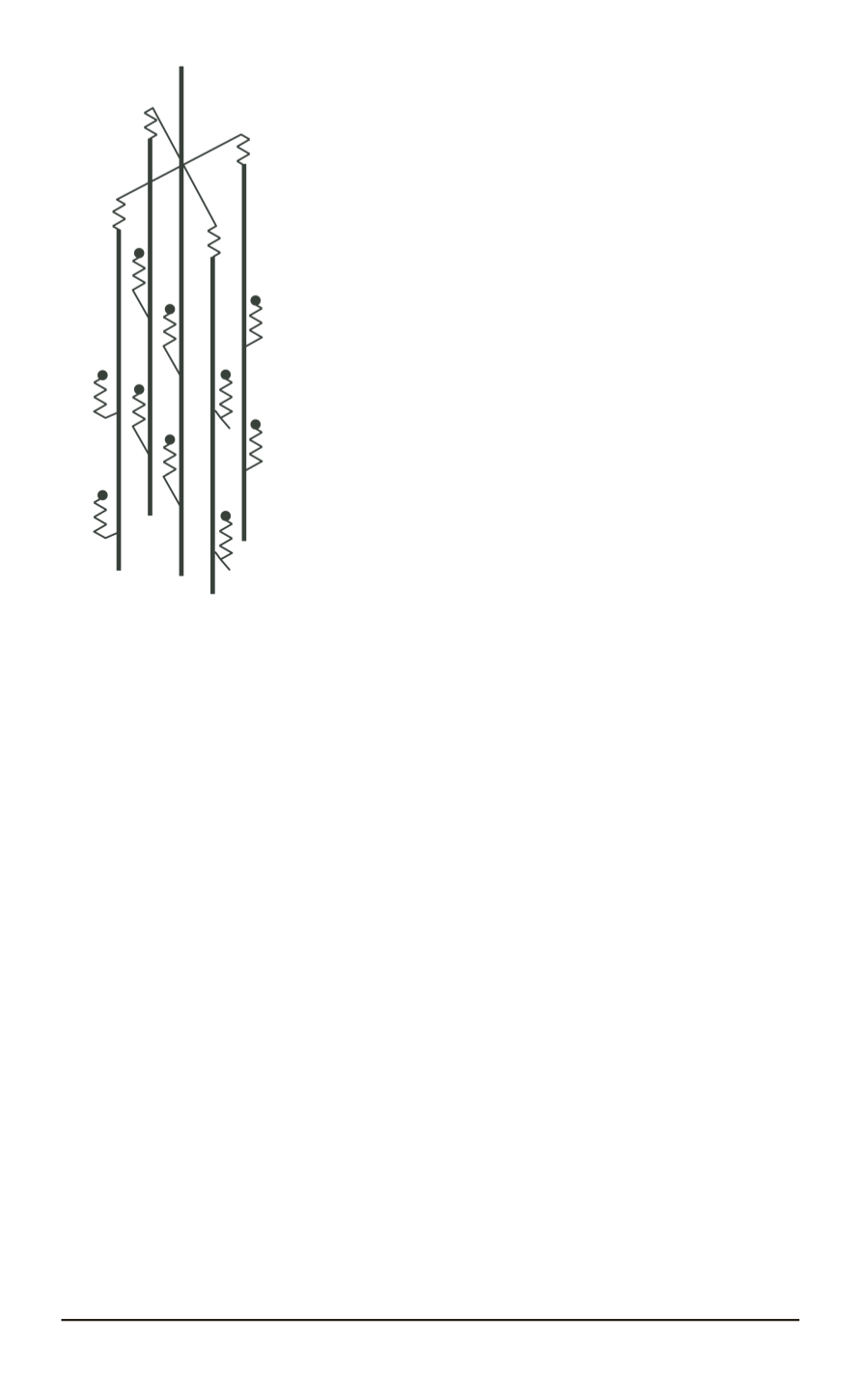
Рис. 5. Расчетная схема
ракеты для анализа про-
дольных колебаний
При расчете собственных частот использо-
вались параметры, типичные для ракет тяже-
лого класса. В результате расчета были полу-
чены следующие парциальные частоты осцил-
ляторов: для баков “Г” (нижние осцилляторы)
f
= 9
,
64
Гц, для баков “О” (верхние осцилля-
торы)
f
= 5
,
36
Гц.
Расчет проводился методом конечных эле-
ментов с помощью решателя NASTRAN. При
решении использовались стержневые элемен-
ты типа СROD, осцилляторы моделировались
элементами сосредоточенной массы СMASS и
соединялись со стержнями упругими элемен-
тами СELAS. Боковые стержни соединялись с
центральным также элементами СELAS. Рас-
чет собственных значений частот проводился
методом Ланцоша для свободного тела.
Далее приведены результаты расчета: зна-
чения первых шести собственных частот
f
=
ω/
2
π
(Гц) — 2,93; 3,80; 6,63; 6,80; 6,92;
10,59 и соответствующие им формы (рис. 6).
Отметим, что рассматриваемая система не
закреплена, но имеется и “нулевой” корень задачи о собственных ко-
лебаниях, соответствующий движениям всего пакета при отсутствии
упругих деформаций, т.е.
U
=
const.
Как следует из полученных значений, низшие частоты колебаний
весьма близки друг к другу. С последующим ростом частоты колеба-
ний осцилляторы перестают в значительной мере влиять на колебания
системы. Для исследования колебаний на более высоких частотах не-
обходимо введение в систему осцилляторов, моделирующих высшие
тона колебания жидкости в баках.
Из рис. 6,
а
следует, что при первой форме колебаний центральный
блок полностью неподвижен, а колебания совершают боковые блоки,
при этом их силовое воздействие на центральный равно нулю. Дан-
ная частота является кратной (здесь представлена форма, при которой
блоки колеблются попарно в противофазе).
Из формы, изображенной на рис. 6,
б
, следует, что колебания со-
вершают все блоки, при этом боковые блоки колеблются с одинако-
вой формой в фазе. Первая и вторая формы колебаний соответствуют
формам, близким к тем, которые наблюдались, если бы блоки бы-
ли неупругими (присутствует значительное перемещение центра масс
каждого блока).
20 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2015. № 5

















