
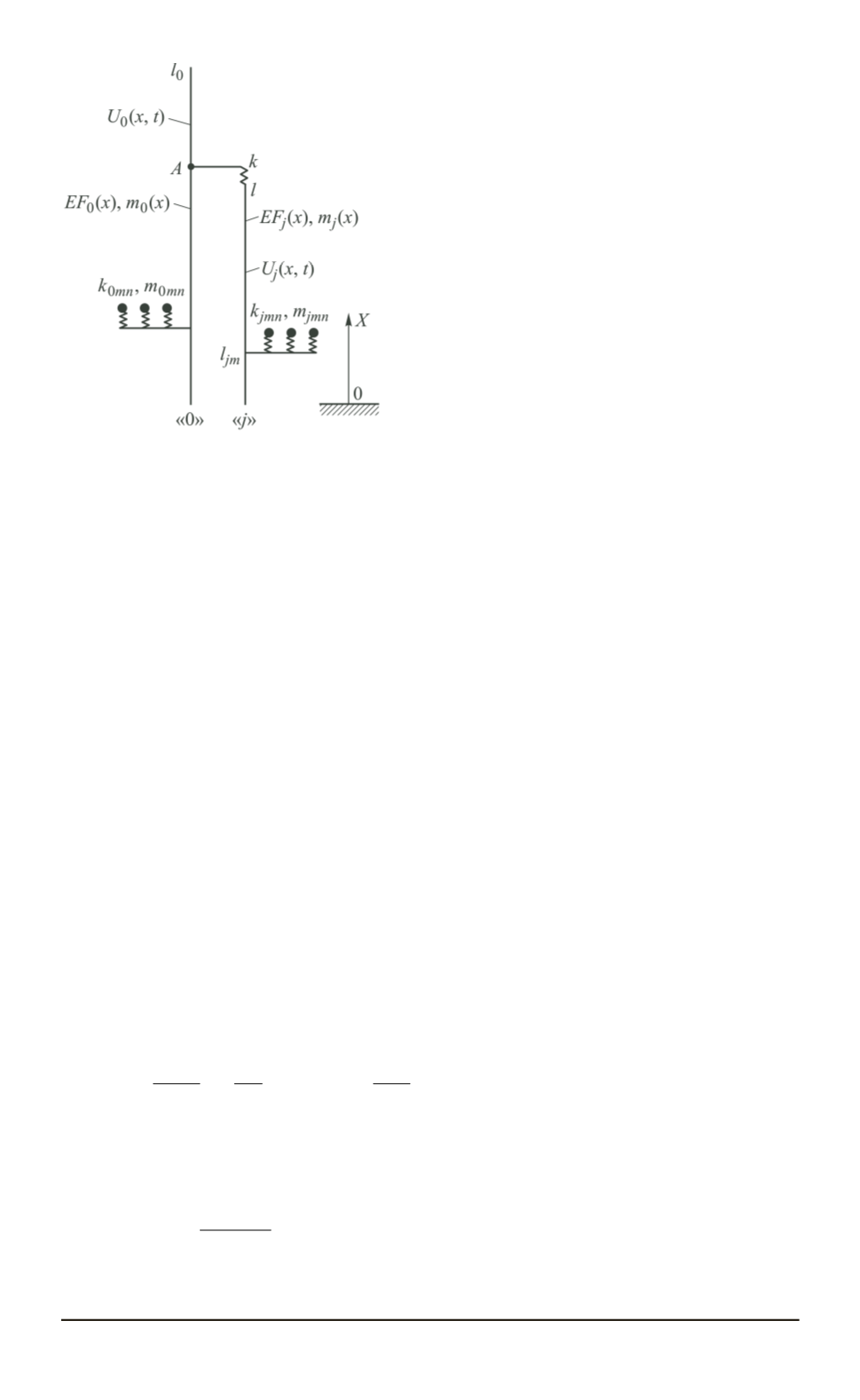
Рис. 4. Расчетная модель продоль-
ных колебаний ракеты пакетной
схемы с произвольным числом
блоков
в ракетах пакетной схемы осуще-
ствляется в верхнем силовом поясе.
Учет колеблющейся массы жидкости
в баках обеспечим введением осцил-
ляторов, закрепленных на уровне си-
ловых шпангоутов днищ соответству-
ющих баков. Для каждого тона коле-
баний жидкости вводится один осцил-
лятор.
Постановка задачи о продоль-
ных колебаниях
. Рассмотрим про-
дольные колебания стержневой си-
стемы, состоящей из центрального
стержня длиной
l
0
и
N
боковых
стержней одинаковой длины
l
j
=
l
(
l
0
> l
,
j
= 1
,
2
, . . . , N
)
, скрепленных
в т.
А
(
x
A
=
l
)
(рис. 4) с центральным
упругим элементом жесткости
k
. В точках с координатой
l
jm
прикреп-
ляется необходимое для конкретного расчетного случая число осцил-
ляторов, моделирующих колебания жидкости. Индексы в параметрах
жесткости
k
jmn
и массы
m
jmn
имеют следующий смысл: индекс
j
обозначает принадлежность к
j
-му стержню,
m
— точку крепления
осциллятора,
n
— номер осциллятора в данной точке крепления.
Введем неподвижную систему отсчета
ОX
и предположим, что
жесткость стержней
EF
j
(
x
)
, распределенная масса
m
j
(
x
)
и возмуще-
ние
q
(
x, t
)
являются ограниченными функциями координаты
x
:
0
< r
j
≤
EF
j
; (
x
)
≤
R
j
;
0
< m
j
≤
m
j
(
x
)
≤
M
j
,
j
= 0
,
1
,
2
, . . . , N
;
0
< q
j
≤
q
j
(
x, t
)
≤
Q
j
.
(1)
Пусть при продольных колебаниях в сечениях стержней с коорди-
натой
x
возникают смещения
u
j
(
x, t
)
, определяемые уравнениями
m
j
(
x
)
∂
2
u
j
∂t
2
−
∂
∂x
EF
j
(
x
)
∂u
j
∂x
=
q
j
(
x, t
)
, j
= 0
,
1
,
2
, . . . , N.
(2)
Уравнение, описывающее смещение массы осциллятора
u
∗
jmn
(
t
)
,
для данной системы запишется следующим образом:
m
jmn
d
2
u
∗
jmn
dt
2
+
k
jmn
u
∗
jmn
−
u
j
(
l
jm
, t
) =
f
jmn
(
t
) ;
j
= 0
,
1
,
2
, . . . , N, m
= 1
,
2
, . . . , N
j
, n
= 1
,
2
, . . . , N
jm
.
(3)
18 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2015. № 5

















