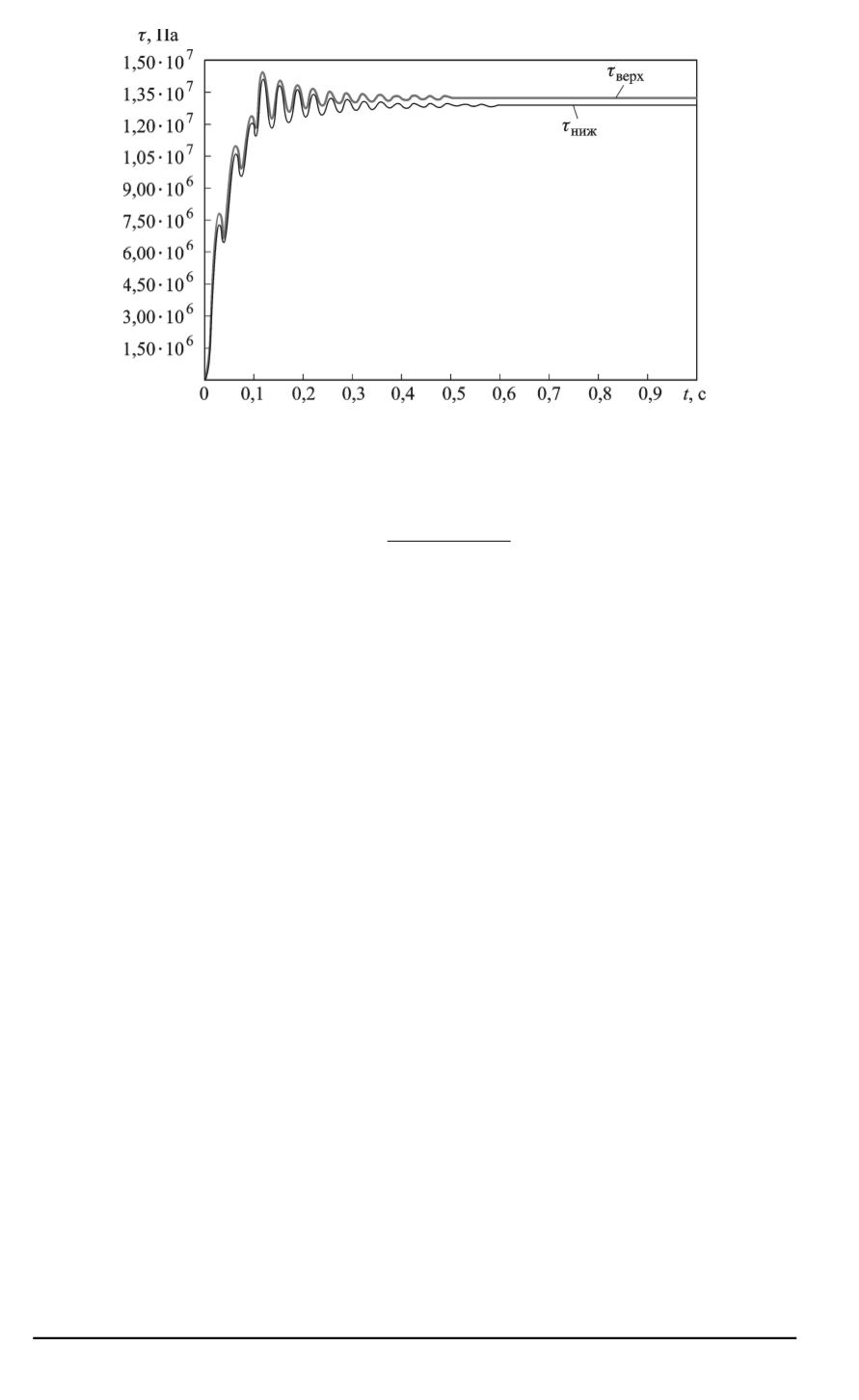
Рис. 4. Графики нагружения шеек рабочих валков
определяется по формуле [5]
N
заг
=
a
кор
τ
m
– 1дет
N
0
n
X
i
=1
τ
m
вред
i
,
(11)
где
a
кор
— корректирующий коэффициент;
τ
– 1дет
— предел выносливо-
сти детали;
m, N
0
— параметры кривой усталости для материала де-
тали;
τ
вред
— амплитуда очередного повреждающего цикла напряжений
[6]. После обработки компьютерных графиков (см. рис. 4) поврежда-
ющие циклы не обнаружены.
Выводы.
1. Составлена расчетная схема линии привода реального
прокатного стана, которая представлена трехмассовой диссипативной
крутильно-колебательной моделью, имеющей постоянную разветвлен-
ную структуру.
2. Инерционно-жесткостные параметры динамической модели
идентифицированы по геометрическим и инерционным характери-
стикам конструкционных элементов. Выполнено необходимое приве-
дение указанных параметров к валу электродвигателя через переда-
точное отношение редуктора. Определены собственные частоты и их
формы для колебаний системы.
3. Определен характер изменения внешних нагрузок. Обоснован
вид математического описания момента электродвигателя и экспонен-
циально-линейный вид момента технологического сопротивления.
4. Составлены уравнения движения крутильно-колебательной си-
стемы на основании уравнений Лагранжа второго рода.
5. Уравнения движения решены на ЭВМ (в среде MathCAD) мето-
дом Рунге–Кутта.
92 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2012. № 4


