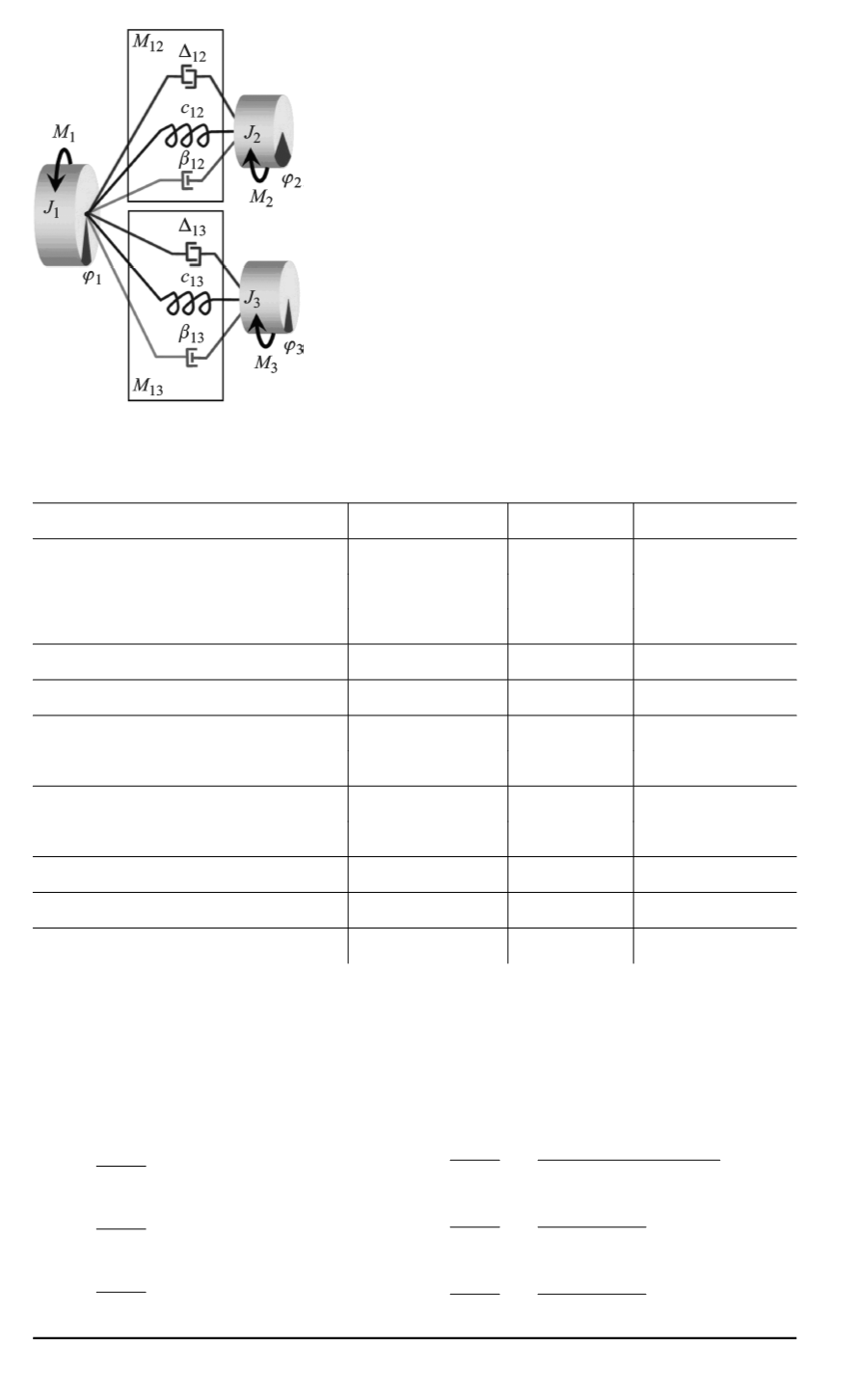
Рис. 2. Расчетная схема:
1, 2, 3
— массивные элементы;
J
1
,
J
2
,
J
3
— мо-
менты инерции;
с
12
,
с
13
— крутильные жесткости;
β
12
,
β
13
— коэффициенты демпфирования;
Δ
12
,
Δ
13
— зазоры;
ϕ
1
,
ϕ
2
,
ϕ
3
— текущие угловые ко-
ординаты;
М
1
— момент электродвигателя;
М
2
,
М
3
— моменты прокатки на верхнем и нижнем
рабочих валках; массивный диск 1 = ротор + муф-
та моторная +шестерня + зубчатое колесо + муфта
коренная; массивный диск 2 = верхний шестерен-
ный валок + верхний шпиндель + верхний рабо-
чий валок; массивный диск 3 = нижний шестерен-
ный валок + нижний шпиндель + нижний рабочий
валок; участок
1–2
— валопровод от ротора до
верхнего рабочего валка; участок
1–3
— валопро-
вод от ротора до нижнего рабочего валка
Исходные данные для моделирования
Параметр
Обозначение Значение Ед. измерения
J
1
32,9
кг
∙
м
2
Момент инерции
J
2
0,9
кг
∙
м
2
J
3
0,9
кг
∙
м
2
Жесткость
с
12
29 600
Н
∙
м/рад
с
13
29 600
Н
∙
м/рад
Коэффициент демпфирования
β
12
20
Н
∙
м
∙
с/рад
β
13
15
Н
∙
м
∙
с/рад
Зазор
Δ
12
0,01
рад
Δ
13
0,005
рад
Момент прокатки
М
прок
5 000
Н
∙
м
Время захвата заготовки
t
зах
0,006
c
Угловая скорость ротора
ω
рот
104,72
рад /с
Уравнения движения крутильно-колебательной системы составле-
ны на основании уравнений Лагранжа второго рода [2]:
J
1
d
2
ϕ
1
dt
2
+
M
12
+
M
13
=
M
1
;
J
2
d
2
ϕ
2
dt
2
−
M
12
=
−
M
2
;
J
3
d
2
ϕ
3
dt
2
−
M
13
=
−
M
3
или
d
2
ϕ
1
dt
2
=
M
1
−
M
12
−
M
13
J
1
;
d
2
ϕ
2
dt
2
=
M
12
−
M
2
J
2
;
d
2
ϕ
3
dt
2
=
M
13
−
M
3
J
3
,
(1)
88 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2012. № 4


