
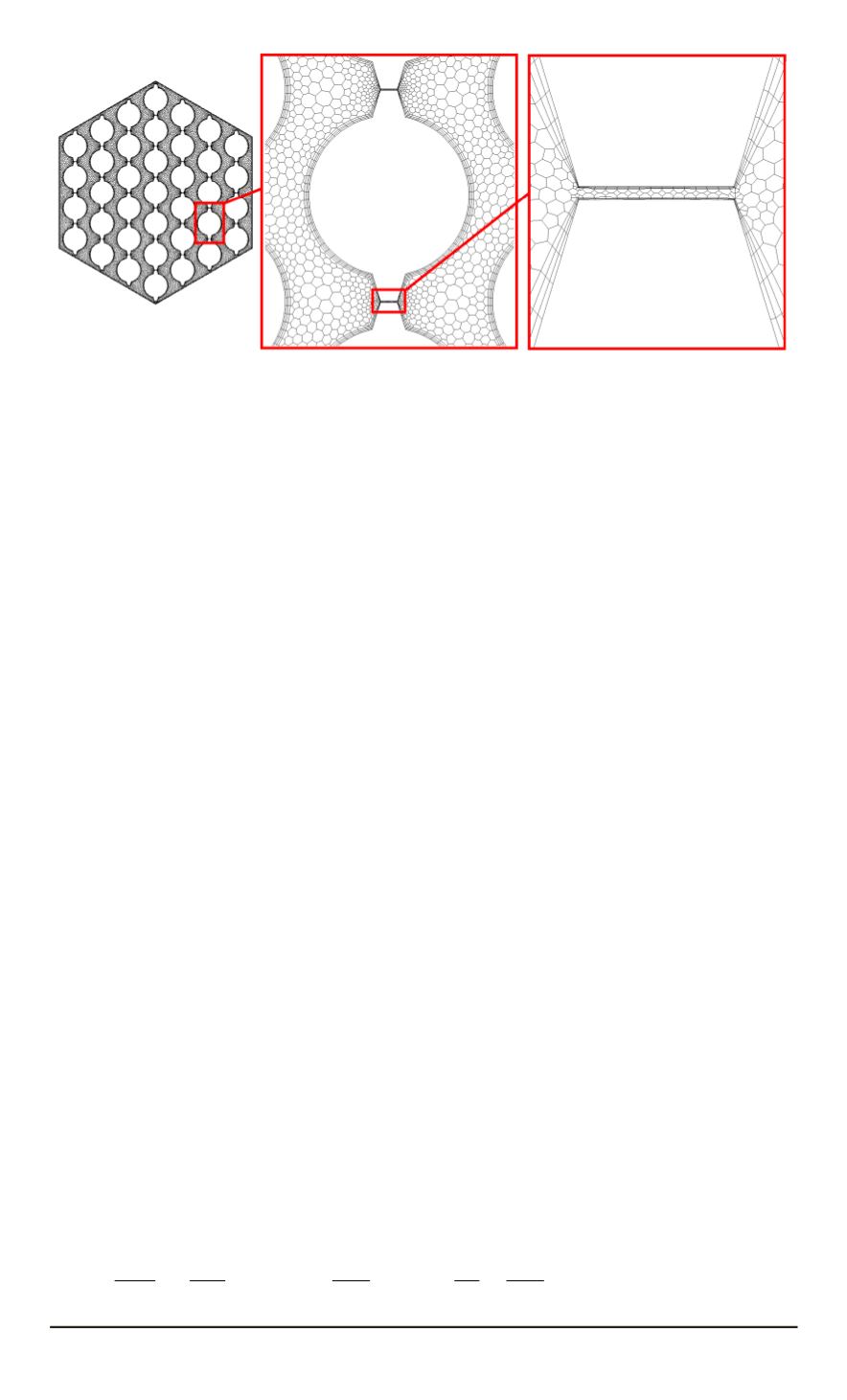
Рис. 1. Фрагменты расчетной сетки модели макета ТВС ЦЗ
Для двух режимов течения в макетах ТВС ЦЗ и ПЗ, реализованных
экспериментально, выполнено численное моделирование с использо-
ванием CFD-пакета ANSYS Fluent 14.5 [9].
Расчетная сетка моделей макетов ТВС ЦЗ и ПЗ построена в два
этапа. На первом этапе с использованием пакета ANSYS Meshing [10]
строилась тетраэдральная расчетная сетка. На втором этапе с исполь-
зованием функций работы с расчетной сеткой ANSYS Fluent выполне-
ны адаптация и конвертация тетраэдральной сетки в полиэдральную.
Общее число элементов расчетной сетки составило
∼
10
8
. Фрагменты
расчетной сетки модели макета ТВС ЦЗ показаны на рис. 1.
В расчетной модели макета ТВС заданы следующие граничные
условия: равномерное распределение расхода по входному сечению
макета и постоянство статического давления потока в выходном сече-
нии. Рабочим телом является воздух, свойства которого определены
законом идеального газа.
При анализе течения в пучках стержней было рассмотрено 7 моде-
лей турбулентности, доступных в пакете ANSYS Fluent [9]: стандарт-
ные (
k
−
ε
)- и (
k
−
ω
)-модели, Realizable–(
k
−
ε
)-, RNG–(
k
−
ε
)- и SST–
(
k
−
ω
)- (модель Ментора), SA- (модель Спаларта – Аллмараса) и RSM-
модели (модель рейнольдсовых напряжений). Выбор данных моделей
обусловлен следующими соображениями.
Стандартная (
k
−
ε
)-модель [9, 11] использует два дифференциаль-
ных уравнения переноса для кинетической энергии турбулентности
k
и скорости диссипации кинетической энергии турбулентности
ε
, кото-
рые получены из уравнений Навье – Стокса и Рейнольдса с использо-
ванием некоторого числа допущений и гипотез [11].
Уравнения переноса без учета влияния плавучести и дополнитель-
ных источников генерации и порождения диссипации турбулентности
записываются в следующем виде:
∂ρk
∂t
+
∂
∂x
i
(
ρku
i
) =
∂
∂x
j
μ
+
μ
t
σ
k
∂k
∂x
j
+
G
k
−
ρε
−
Y
k
;
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение” 2015. № 2 7

















