
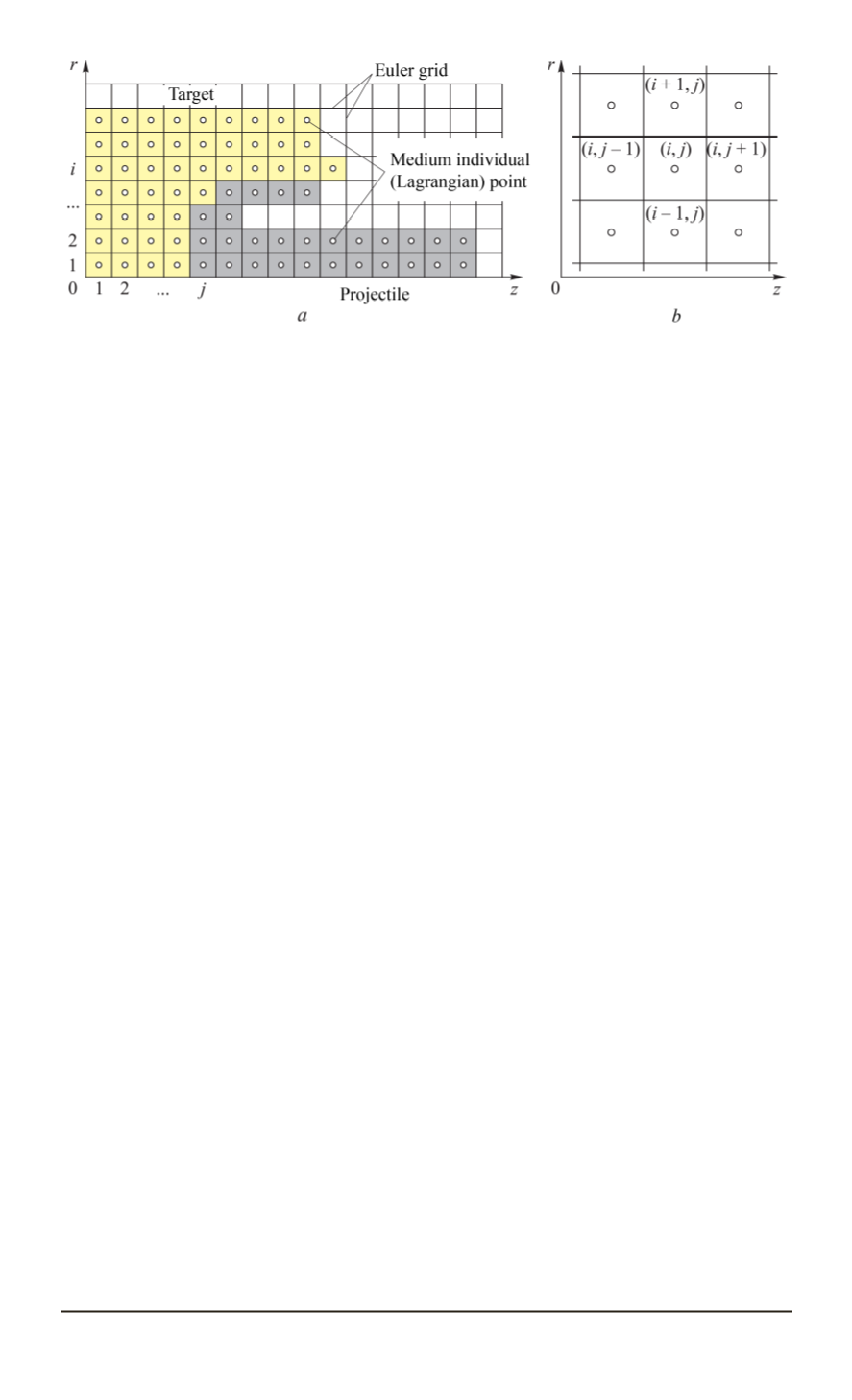
Fig. 1. Computational scheme of the free Lagrangian points method:
a
— discretization of the computational area;
b
— finite-difference scheme template
Pressure inside the metals as a function of volumetric deformation
(density ratio
ρ/ρ
0
) is often calculated by the barotropic equation [3]:
p
=
A
((
ρ/ρ
0
)
n
−
1)
,
(1)
here
ρ
0
is material density at normal conditions (at zero pressure);
A, n
are empirical constants of the material. When metal projectiles interact
with the metal targets at velocities with the order of one to two kilometers
per second, the influence of material internal energy on pressure can be
neglected.
Boundary conditions of the problem in question (Fig. 1,
a
) are as
follows. It is assumed that on the axis of symmetry (
r
= 0
) there is no
radial component of the medium particle velocity (
v
r
= 0
). Mechanical
stresses on the free surfaces of the target and projectile materials are
assumed to be zero. On the contact surface of both the projectile and the
target, normal and tangential stresses in the interacting materials must be
equal to each other.
After setting the initial conditions it is assumed that the target material
is at rest and is not disturbed (velocities and all components of the stress-
strain state are zero). At the initial moment the projectile material is also
assumed to be undisturbed (all components of the stress-strain state are
zero). In addition to that the same velocity
v
0
oriented along
z
axis is set
at
t
= 0
for the whole volume of the projectile material.
For numerical solution to the formulated problem, a computational
algorithm is used, which is based on the method of free Lagrangian
points [7, 8].
The basic concept of the numerical method is as follows [9]. In the
computational area, a fixed Euler mesh is introduced. It has orthogonal
cells of the size
Δ
r
in the radial direction and
Δ
z
in the axial direction (see
Fig. 1,
a
). Some individual (Lagrangian) points of the medium are placed
into these Euler mesh cells, which are located inside the computational
68 ISSN 0236-3941. HERALD of the BMSTU Series “Mechanical Engineering”. 2015. No. 1

















